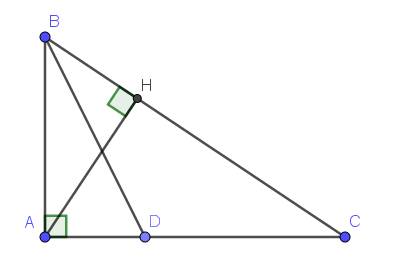
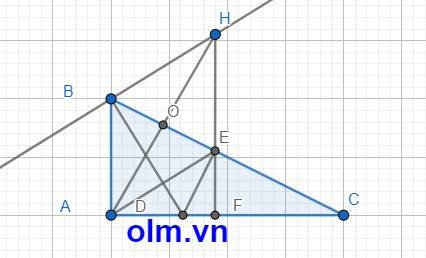
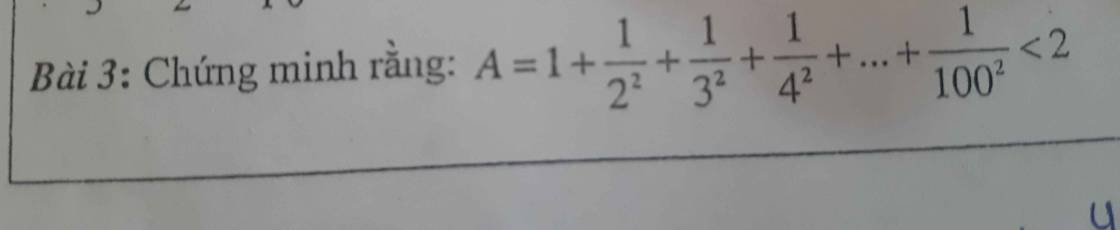Cho tam giác ABC cân tại A.Trên cạnh BC lấy điểm D.Trên tia đối của tia CB lấy E sao cho BD=CE.Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N.Chứng minh
a)DM=EN
b)Đg thẳng BC cắt MN tại điểm I là trung điểm của MN. Kẻ AH vuông góc với BC,(H thuộc BC).Đường thẳng vuông góc với MN tại I cắt đường thẳng AH tại O. Chứng minh tam giác OAB = tam giác OAC và tam giác OBM=tam giác OCN
c)OC vuông góc với AC