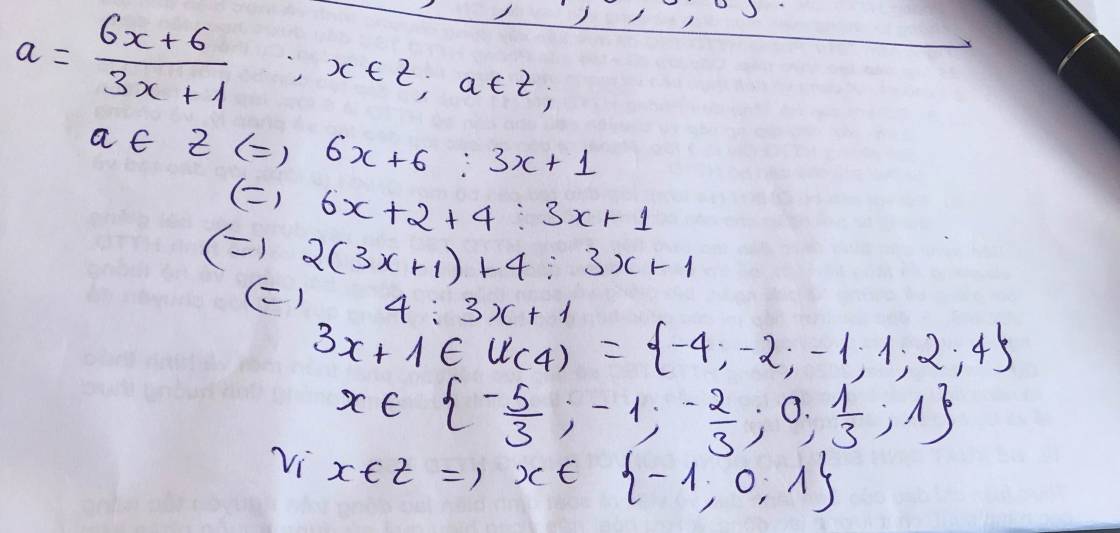
Để giải bài toán này, ta cần xác định chu vi và diện tích của mảnh bìa hình chữ nhật.

Gọi chiều dài của mảnh bìa hình chữ nhật là \(a\) (cm) và chiều rộng là \(b\) (cm).

Ta có các điều kiện sau:
1. Chu vi của hình chữ nhật: \(2(a + b)\)
2. Chu vi của hình vuông: \(4 \times \text{cạnh}\)

Theo đề bài:
- Chu vi hình chữ nhật bằng chu vi hình vuông: \(2(a + b) = 4 \times 6 \) (vì cạnh hình vuông là 6cm).

- Chiều dài hơn chiều rộng 6cm: \(a = b + 6\).

Giải hệ phương trình để tìm \(a\) và \(b\):
1. Từ phương trình 1: \(2(a + b) = 4 \times 6\), ta có: \(a + b = 12\).

2. Thay \(a = b + 6\) vào phương trình 1:
\( (b + 6) + b = 12 \),
\(2b + 6 = 12\),
\(2b = 6\),
\(b = 3\).

3. Từ \(b = 3\), ta tính \(a\):
\(a = b + 6 = 3 + 6 = 9\).

Sau khi tìm được \(a = 9\) và \(b = 3\), ta tính diện tích mảnh bìa hình chữ nhật:
Diện tích \(= a \times b = 9 \times 3 = 27 \, \text{cm}^2\).

Vậy, diện tích của mảnh bìa đó là \(27 \, \text{cm}^2\).

Để giải bài toán này, ta cần xác định chu vi và diện tích của mảnh bìa hình chữ nhật.

Gọi chiều dài của mảnh bìa hình chữ nhật là �a (cm) và chiều rộng là �b (cm).

Ta có các điều kiện sau:

1. Chu vi của hình chữ nhật: 2(�+�)2(a+b)
2. Chu vi của hình vuông: 4×cạnh4×cạnh

Theo đề bài:

• Chu vi hình chữ nhật bằng chu vi hình vuông: 2(�+�)=4×62(a+b)=4×6 (vì cạnh hình vuông là 6cm).

• Chiều dài hơn chiều rộng 6cm: �=�+6a=b+6.

Giải hệ phương trình để tìm �a và �b:

1. Từ phương trình 1: 2(�+�)=4×62(a+b)=4×6, ta có: �+�=12a+b=12.

2. Thay �=�+6a=b+6 vào phương trình 1: (�+6)+�=12(b+6)+b=12, 2�+6=122b+6=12, 2�=62b=6, �=3b=3.

3. Từ �=3b=3, ta tính �a: �=�+6=3+6=9a=b+6=3+6=9.

Sau khi tìm được �=9a=9 và �=3b=3, ta tính diện tích mảnh bìa hình chữ nhật: Diện tích =�×�=9×3=27 cm2=a×b=9×3=27cm2.

Vậy, diện tích của mảnh bìa đó là 27 cm227cm2.

Phân số `19/8 ` được viết dưới dạng số thập phân có phần nguyên là:

A. 2                                 C. 357

B. 3                                 D. Không viết được dưới dạng thập phân

A.2

Do góc xoz =60^o

mà Om là tia pgiac của \(\widehat{zox}\)

=>\(\widehat{zOm}=\widehat{mOx}=\dfrac{60}{2}=30^o\)

Ta có: \(\widehat{yOz}+\widehat{xOz}=100^o\) (do 2 góc kề bù)

=> \(\widehat{yOz}=100^o-\widehat{xOz}\\ =100^o-60^o=40^o\)

Mà On là tia phân giác \(\widehat{yOz}\)

=>\(\widehat{yOn}=\widehat{nOz}=\widehat{yOz}:2=40^o:2=20^o\)

\(\Rightarrow\widehat{mOn}=\widehat{nOz}+\widehat{zOm}=20^o+30^o=50^o\)

Vậy góc mOn=50^o

Để tính số đo của góc ∠���∠MON, ta sử dụng các thông tin đã cho:

Góc ∠���∠xOy có số đo là 100 độ.

1. Góc ∠���∠xOz có số đo là 60 độ.

Do ∠���=∠���+∠���∠xOy=∠xOz+∠zOy, ta có:

100∘=60∘+∠���100∘=60∘+∠zOy.

Từ đó, ta tính được số đo của góc ∠���∠zOy:

∠���=100∘−60∘=40∘∠zOy=100∘−60∘=40∘.

Vì ∠���∠MON là góc phân giác của ∠���∠zOy, nên số đo của ∠���∠MON bằng một nửa số đo của ∠���∠zOy:

∠���=40∘2=20∘∠MON=240∘​=20∘.

Vậy, số đo của góc ∠���∠MON là 20 độ.

7 tiếng

4 giờ là 4h sáng hay 4h tối

help me!

help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!help me!

cứu tui

sos với

mìn cần gấp

\(6\in A;7\notin A;\left\{8;10\right\}\subset A\)

\(y=x^3-3x^2-9x+35\)

\(y'=3x^2-6x-9\)

\(y'=0\Leftrightarrow3x^2-6x-9=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)

\(y\left(-4\right)=-41;y\left(-1\right)=40;y\left(3\right)=8;y\left(4\right)=52\)

\(\Rightarrow y_{max}=y\left(4\right)=52;y_{min}=y\left(-4\right)=-41\) trên đoạn \(\left[-4;4\right]\)