Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(VT=\sqrt{4-x}+\sqrt{x-2}\le\sqrt{2\left[\left(\sqrt{4-x}\right)^2+\left(\sqrt{x-2}\right)^2\right]}=2\) (1)
\(VP=x^2-6x+11=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2\ge2\) (2)
Từ (1) và (2) ta có dấu "=" xảy ra:
\(\left\{{}\begin{matrix}4-x=x-2\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\x=3\end{matrix}\right.\Leftrightarrow x=3\)
Vậy: ..
\(\left(x+2\right)^2-\left(2x+1\right)\left(x+2\right)=0\\ < =>\left(x+2\right)\left[\left(x+2\right)-\left(2x+1\right)\right]=0\\ < =>\left(x+2\right)\left(x+2-2x-1\right)=0\\ < =>\left(x+2\right)\left(1-x\right)=0\\ < =>\left[{}\begin{matrix}x+2=0\\1-x=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Vậy: ...
\(\left(x+2\right)^2-\left(2x+1\right)\left(x+2\right)=0\)
=>(x+2)(x+2-2x-1)=0
=>(x+2)(-x+1)=0
=>\(\left[{}\begin{matrix}x+2=0\\-x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
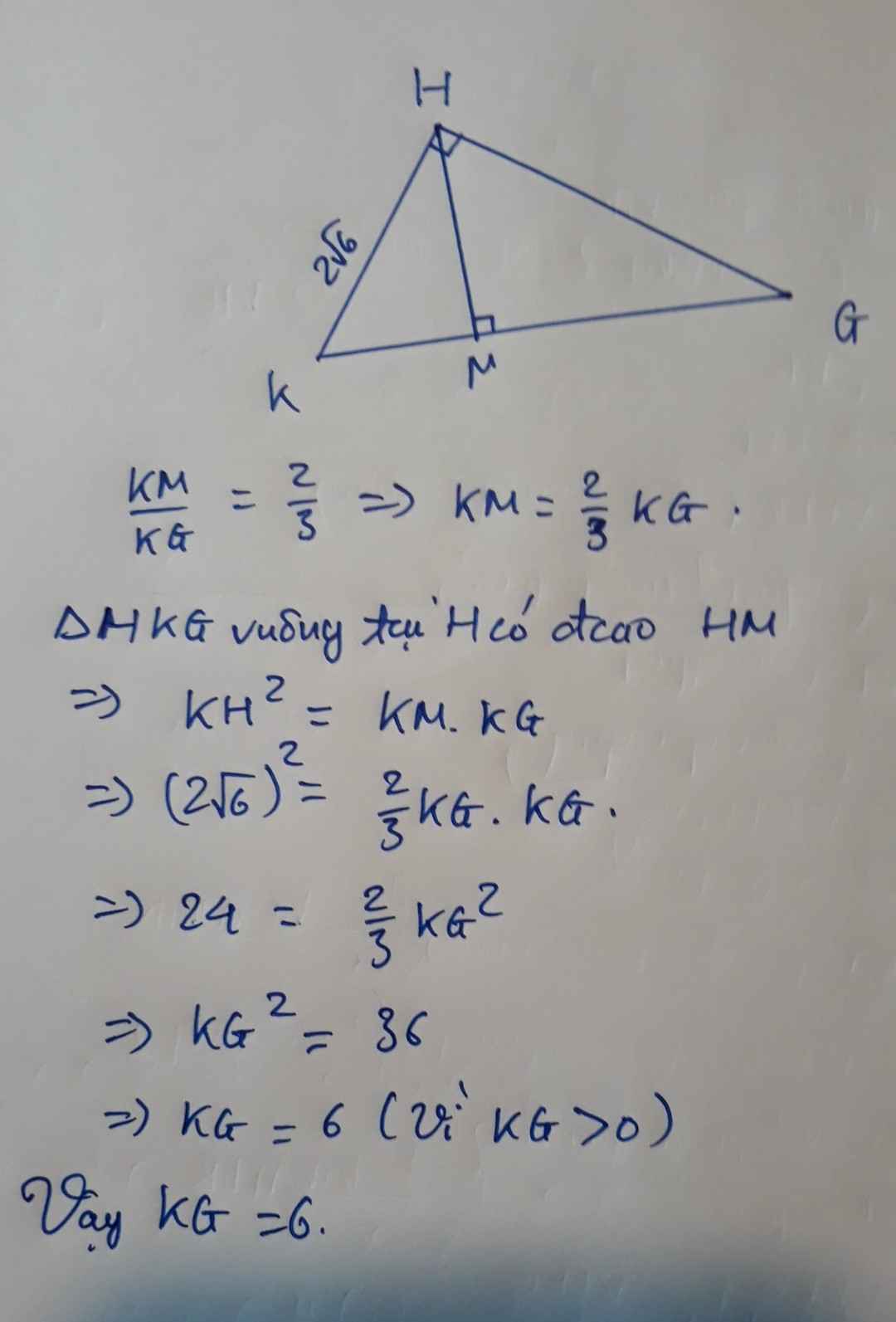
A và B chia hết cho C
Ta có:
\(\dfrac{A}{C}=\dfrac{12x^{2n}y^{12-3n}}{3x}=4x^{2n-1}y^{12-3n}\)
\(\dfrac{B}{C}=\dfrac{x^3y^7}{3x}=\dfrac{1}{3}x^2y^7\)
Để A và B chia hết cho C thì: \(\left\{{}\begin{matrix}2n-1\ge0\\12-3n\ge0\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}\le n\le4\)
Mà: n thuộc Z => n ∈ {1; 2; 3; 4}
Lần sau em cần gõ đề bài bằng công thức toán học có biểu tượng \(\Sigma\) bên trái màn hình em nhé.
Để hpt có nghiệm thì:
\(\dfrac{m}{4}\ne\dfrac{1}{-m}\Leftrightarrow m^2\ne-4\Leftrightarrow m\in R\)
\(\left\{{}\begin{matrix}mx+y=5\\4x-my=1\end{matrix}\right.< =>\left\{{}\begin{matrix}m^2x+my=5m\\4x-my=1\end{matrix}\right.< =>\left\{{}\begin{matrix}\left(m^2+4\right)x=5m+1\\mx+y=5\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x=\dfrac{5m+1}{m^2+4}\\\dfrac{5m^2+m}{m^2+4}+y=5\end{matrix}\right.< =>\left\{{}\begin{matrix}x=\dfrac{5m+1}{m^2+4}\\y=5-\dfrac{5m^2+m}{m^2+4}\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x=\dfrac{5m+1}{m^2+4}\\y=\dfrac{5m^2+20-5m^2-m}{m^2+4}\end{matrix}\right.< =>\left\{{}\begin{matrix}x=\dfrac{5m+1}{m^2+4}\\y=\dfrac{20-m}{m^2+4}\end{matrix}\right.\)
Ta có:
\(2y=1-x=>2\cdot\dfrac{20-m}{m^2+4}=1-\dfrac{5m+1}{m^2+4}\\ \Leftrightarrow\dfrac{40-2m}{m^2+4}=\dfrac{m^2+4-5m-1}{m^2+4}\\ \Leftrightarrow40-2m=m^2-5m+3\\ \Leftrightarrow m^2-5m+3+2m-40=0\\ \Leftrightarrow m^2-3m-37=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot\left(-37\right)=157>0\\ m_1=\dfrac{3+\sqrt{157}}{2}\\ m_2=\dfrac{3-\sqrt{157}}{2}\)
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
=>\(AE\cdot AC=AF\cdot AB\)
b: Xét ΔADB vuông tại D có DM là đường cao
nên \(AM\cdot AB=AD^2\left(1\right)\)
Xét ΔADC vuông tại D có DN là đường cao
nên \(AN\cdot AC=AD^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=>\(\dfrac{AN}{AM}=\dfrac{AE}{AF}\)
=>\(\dfrac{AE}{AN}=\dfrac{AF}{AM}\)
=>\(AN\cdot AF=AM\cdot AE\)
c: Xét ΔANM có \(\dfrac{AE}{AN}=\dfrac{AF}{AM}\)
nên EF//MN