Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\\ < =>\left(x+\sqrt{3+x^2}\right)\left(x-\sqrt{3+x^2}\right)\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>x^2-3-x^2\left(y+\sqrt{3+y^2}\right)=3\left(x-\sqrt{3+x^2}\right)\\ < =>-\left(y+\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}\left(1\right)\)
Tương tự ta có: \(x+\sqrt{3+x^2}=-\left(y-\sqrt{3+y^2}\right)\left(2\right)\)
Lấy (1) + (2) ta có:
\(-\left(y+\sqrt{3+y^2}\right)-\left(y-\sqrt{3+y^2}\right)=x-\sqrt{3+x^2}+x+\sqrt{3+x^2}\\ < =>-2y=2x\\ < =>2x+2y=0\\ < =>x+y=0\)

\(\left(a\right)\dfrac{5}{3}-\dfrac{1}{2}:x=\dfrac{2}{7}\\ \dfrac{1}{2}:x=\dfrac{5}{3}-\dfrac{2}{7}=\dfrac{29}{21}\\ x=\dfrac{1}{2}:\dfrac{29}{21}=\dfrac{21}{58}\\ \left(b\right)\dfrac{1}{4}\cdot x+\dfrac{7}{5}=\dfrac{5}{3}\\ \dfrac{1}{4}\cdot x=\dfrac{5}{3}-\dfrac{7}{5}=\dfrac{4}{15}\\ x=\dfrac{4}{15}:\dfrac{1}{4}=\dfrac{16}{15}\\ \left(c\right)5\cdot x-2024=3\cdot x\\ 5\cdot x-3\cdot x=2024\\ x\cdot\left(5-3\right)=2024\\ x\cdot2=2024\\ x=2024:2=1012\)

\(\dfrac{x}{8}\) + \(\dfrac{2}{3}\) = \(\dfrac{7}{6}\)
\(\dfrac{x}{8}\) = \(\dfrac{7}{6}\) - \(\dfrac{2}{3}\)
\(\dfrac{x}{8}\) = \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{1}{2}\) x 8
\(x\) = 4
\(\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\)
\(\dfrac{x}{8}=\dfrac{7}{6}-\dfrac{2}{3}\)
\(\dfrac{x}{8}=\dfrac{1}{2}=\dfrac{4}{8}\)
⇒ x = 4
Vậy x = 4

\(\overline{ab8}+\overline{ab}=949\\ \overline{ab}\times10+8+\overline{ab}=949\\\overline{ab} \times\left(10+1\right)=949-8\\ \overline{ab}\times11=941\\ \overline{ab}=941:11\\ \overline{ab}=941:11\\ \overline{ab}=\dfrac{941}{11}\)
Mà: ab là số tự nhiên nên ta loại


\(\dfrac{6}{8}=\dfrac{15}{x}\\ \Rightarrow6\times x=15\times8\\ \Rightarrow6\times x=120\\ \Rightarrow x=120:6\\ \Rightarrow x=20\)
Vậy \(x=20\)
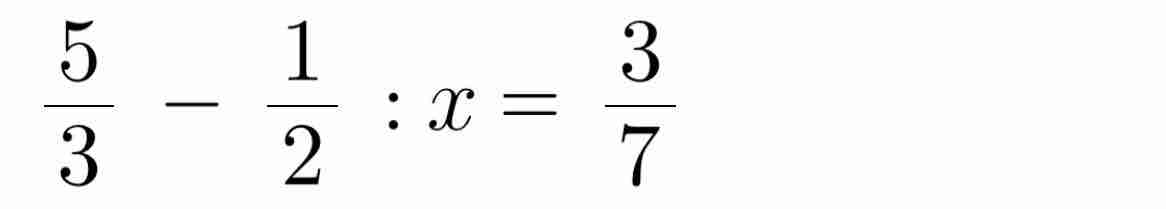
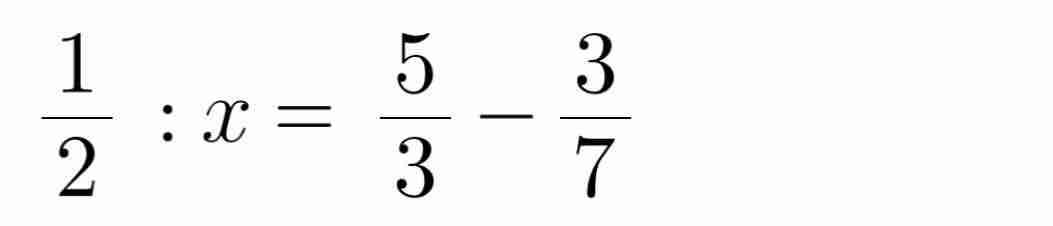
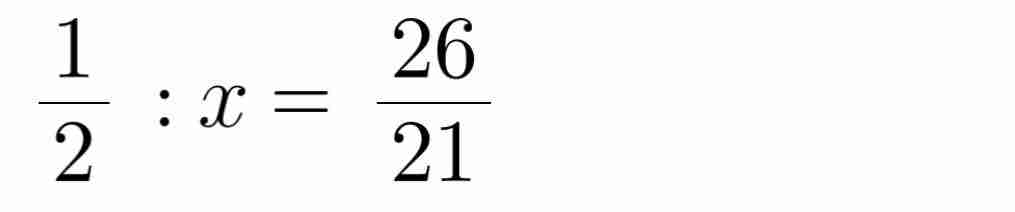

Bài 1:
Số lần bắn được ít nhất 8 điểm là:
5+6+5=16(lần)
=>Xác suất để bắn được ít nhất 8 điểm là \(P=\dfrac{16}{20}=\dfrac{4}{5}\)
Bài 2:
a: Xác suất xuất hiện mặt N là: \(\dfrac{18}{22}=\dfrac{9}{11}\)
b: Số lần xuất hiện mặt S là 25-11=14(lần)
Xác suất xuất hiện mặt S là \(\dfrac{14}{25}\)
c: Xác suất xuất hiện mặt N là \(\dfrac{14}{30}=\dfrac{7}{15}\)