a: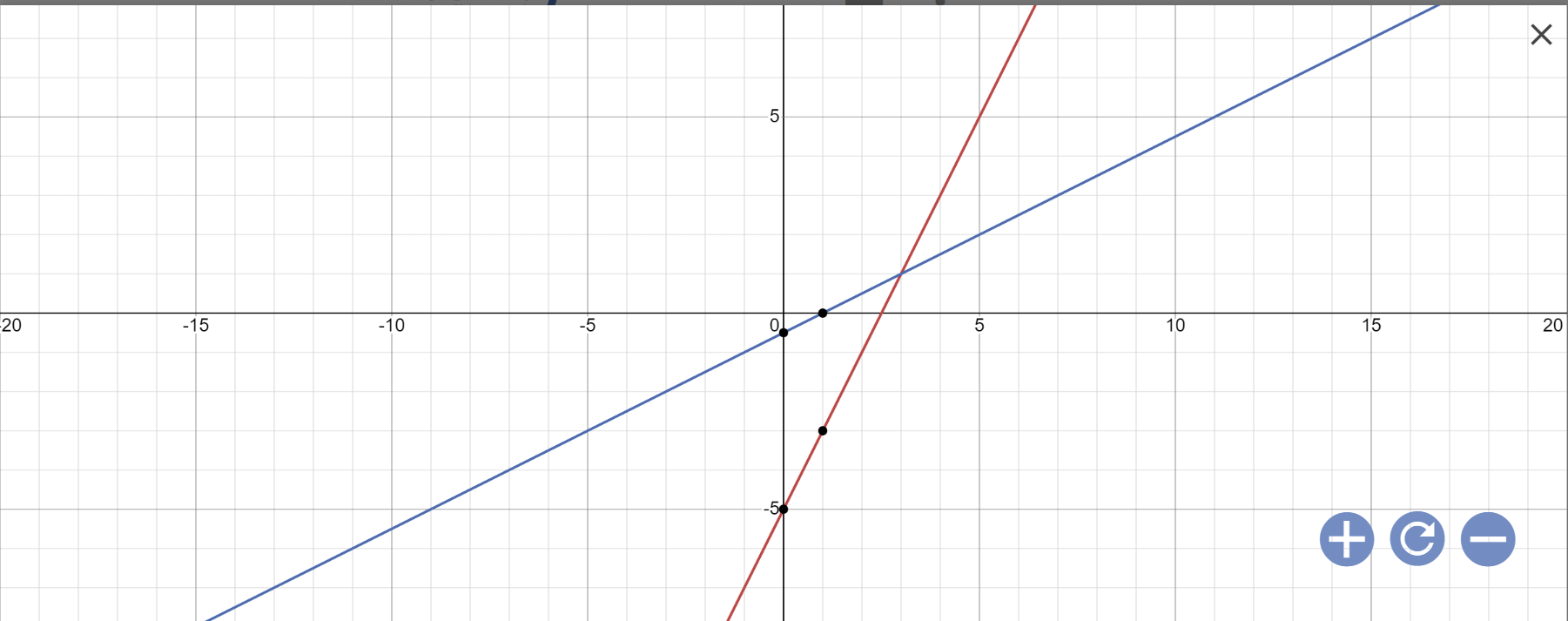 

b: Nghiệm của hệ phương trình\(\left\{{}\begin{matrix}2x-y=5\\x-2y=1\end{matrix}\right.\) chính là giao điểm của (d1),(d2)

Theo đồ thị, ta thấy (d1) cắt (d2) tại A(3;1)

=>Nghiệm của hệ phương trình \(\left\{{}\begin{matrix}2x-y=5\\x-2y=1\end{matrix}\right.\) là \(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)

c: Thay x=3 và y=1 vào (d3), ta được:

\(3m+\left(2m-1\right)\cdot1=3\)

=>5m-1=3

=>5m=4

=>\(m=\dfrac{4}{5}\)

Đề bị thiếu rồi bạn.

Bạn xem lại đề đi có đúng không !!! 

\(90+\left\{20-10+\left[12+78+\left(5^2-15\right)\right]\right\}\)

\(=90+\left\{20-10+\left[12+78+\left(25-15\right)\right]\right\}\)

\(=90+\left\{20-10+\left[12+78+10\right]\right\}\)

\(=90+\left\{20-10+\left[90+10\right]\right\}\)

\(=90+\left\{20-10+100\right\}\)

\(=90+\left\{10+100\right\}\)

\(=90+110\)

\(=200\)

\(#NqHahh\)

$90+\{20-10+[12+78+(5^2-15)]\}$

$=90+10+[90+(25-15)]$

$=100+(90+10)$

$=100+100=200$

Ta có:

\(40=2^3.5\\ 28=2^2.7\\ 140=2^2.5.7\\ \Rightarrow\text{BCNN}\left(40;28;140\right)=2^3.5.7=280\)

BCNN = 4

\(\left(x^2-4\right)+\left(x-2\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)+\left(x-2\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2+3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(5-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\5-x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

Gọi H là giao điểm của CN với BM

Xét ΔHCB có

CM,BN là các đường cao

CM cắt BN tại A

Do đó: A là trực tâm của ΔHCB

=>HA\(\perp\)CB tại K

Xét ΔBKA vuông tại K và ΔBNC vuông tại N có

\(\widehat{CBN}\) chung

Do đó: ΔBKA~ΔBNC

=>\(\dfrac{BK}{BN}=\dfrac{BA}{BC}\)

=>\(BN\cdot BA=BK\cdot BC\)

Xét ΔCKA vuông tại K và ΔCMB vuông tại M có

\(\widehat{KCA}\) chung

Do đó: ΔCKA~ΔCMB

=>\(\dfrac{CK}{CM}=\dfrac{CA}{CB}\)

=>\(CM\cdot CA=CK\cdot CB\)

\(BA\cdot BN+CA\cdot CM\)

\(=BC\cdot BK+BC\cdot CK=BC\left(BK+CK\right)=BC^2\)

$80+\{20-10.[23+17]+(12+2^3)\}$

$=80+\{20-10.40+(12+8)\}$

$=80+\{20-400+20\}$

$=80+20-400+20$

$=100-400+20$

$=-300+20=-280$

Sao ngoặc tròn lại bên ngoài ngoặc vuông ạ? Bạn xem lại đề bài.

\(30=2\cdot3\cdot5;150=2\cdot3\cdot5^2\)

=>\(BCNN\left(30;150\right)=2\cdot3\cdot5^2=150\)

Ta có:

\(30=2.3.5\)

\(150=2.3.5^2\)

\(BCNN\left(30;150\right)=2.3.5^2=2.3.25=150\)

\(#NqHahh\)

\(\left(\dfrac{1}{1.2}+\dfrac{2}{2.4}+\dfrac{2}{4.6}+\dots+\dfrac{2}{28.30}\right).30-0,2\times\left(x-1\right)=10\\ \left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dots+\dfrac{1}{28}-\dfrac{1}{30}\right).30-0,2\times\left(x-1\right)=10\\ \left(1-\dfrac{1}{30}\right).30-0,2\times\left(x-1\right)=10\\ 30-1-0,2\times\left(x-1\right)=10\\ 29-0,2\times\left(x-1\right)=10\\ 0,2\times\left(x-1\right)=29-10\\ 0,2\times\left(x-1\right)=19\\ x-1=19:0,2\\ x-1=95\\ x=95+1=96\)

\(\left(\dfrac{1}{1\cdot2}+\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{28\cdot30}\right)\cdot30-0,2\cdot\left(x-1\right)=10\)

=>\(\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+...+\dfrac{1}{28}-\dfrac{1}{30}\right)\cdot30-0,2\left(x-1\right)=10\)

=>\(\dfrac{29}{30}\cdot30-0,2\left(x-1\right)=10\)

=>\(29-0,2\left(x-1\right)=10\)

=>\(0,2\left(x-1\right)=29-10=19\)

=>x-1=19:0,2=95

=>x=95+1=96

\(\left(2x-3\right)\left(5x+1\right)=\left(3-2x\right)\left(x-5\right)\)

=>\(\left(2x-3\right)\left(5x+1\right)-\left(3-2x\right)\left(x-5\right)=0\)

=>\(\left(2x-3\right)\left(5x+1\right)+\left(2x-3\right)\left(x-5\right)=0\)

=>\(\left(2x-3\right)\left(5x+1+x-5\right)=0\)

=>\(\left(2x-3\right)\left(6x-4\right)=0\)

=>\(2\left(2x-3\right)\left(3x-2\right)=0\)

=>(2x-3)(3x-2)=0

=>\(\left[{}\begin{matrix}2x-3=0\\3x-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{3}\end{matrix}\right.\)

\(\left(2x-3\right)\left(5x+1\right)=\left(3-2x\right)\left(x-5\right)\\ \Leftrightarrow\left(2x-3\right)\left(5x+1\right)+\left(2x-3\right)\left(x-5\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(5x+1+x-5\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(6x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=0\\6x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\6x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{3}\end{matrix}\right.\)