tìm abc chẵn a+b+c=5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thằng Bino đến, bổ sung cho tôi một cách nhìn khác về bạn bè
Bino mở ra cho tôi những kích thước mới của cuộc sống

Gọi số cần tìm là a(a\(\in\)N)
Ta có:
a : 4 dư 1
a : 5 dư 2 \(\Rightarrow\)a - 1 \(⋮\) 4;6\(\Rightarrow\) a \(\in\)BCNN(4;6)
a : 6 dư 1
a nhỏ nhất
4=22;6=2.3
\(\Rightarrow\)BCNN(4;6)=22.3=12
Vì 12 : 5 dư 2
\(\Rightarrow a=12\)
Vậy số cần tìm là 12

Bài 3:
a, (\(x.7\) + 8):5 = 10
\(x\).7 + 8 = 50
\(x\).7 = 50 - 8
\(x.7\) = 42
\(x\) = 42: 7
\(x\) = 6
b, (\(x\) + 5).19: 13 = 57
(\(x\) + 5).19 = 57.13
(\(x\) + 5).19 = 741
\(x\) + 5 = 741: 19
\(x\) + 5 = 39
\(x\) = 39 - 5
\(x\) = 34
c, 4.(36 - 4.\(x\)) = 64
36 - 4.\(x\) = 64:4
36 - 4.\(x\) = 16
4.\(x\) = 36 - 16
4.\(x\) = 20
\(x\) = 5

a, Số tự nhiên có 3 chữ số có dạng: \(\overline{abc}\)
a,b,c lần lượt có số cách chọn là: 9;10;10
Số các số tự nhiên có 3 chữ số là: 9.10.10 = 900 (số)
KL:...
b, Số tự nhiên có 3 chữ số có dạng: \(\overline{abc}\)
a,b,c lần lượt có số cách chọn là: 9; 10; 5
Số các số tự nhiên chẵn có ba chữ số là: 9.10.5 = 450 (số)
Kl:..
c, Số lẻ nhỏ nhất thỏa mãn đề bài là: 21; số lẻ lớn nhất thỏa mãn đề bài là: 345
Số các số thỏa mãn đề bài là: (345 - 21): 2 + 1 = 163 (số)
KL...
a, Số tự nhiên có 3 chữ số có dạng:
�
�
�
‾
abc
a,b,c lần lượt có số cách chọn là: 9;10;10
Số các số tự nhiên có 3 chữ số là: 9.10.10 = 900 (số)
KL:...
b, Số tự nhiên có 3 chữ số có dạng:
�
�
�
‾
abc
a,b,c lần lượt có số cách chọn là: 9; 10; 5
Số các số tự nhiên chẵn có ba chữ số là: 9.10.5 = 450 (số)
Kl:..
c, Số lẻ nhỏ nhất thỏa mãn đề bài là: 21; số lẻ lớn nhất thỏa mãn đề bài là: 345
Số các số thỏa mãn đề bài là: (345 - 21): 2 + 1 = 163 (số)
KL.
Chúc em nha


a) 3x . 3 = 243 Để giải phương trình này, ta chia cả hai vế của phương trình cho 3: 3x = 243 ÷ 3 3x = 81 Sau đó, chia cả hai vế của phương trình cho 3: x = 81 ÷ 3 x = 27
Vậy, giá trị của x là 27.
b) 2x . 162 = 1024 Để giải phương trình này, ta chia cả hai vế của phương trình cho 162: 2x = 1024 ÷ 162 2x = 6.32
Sau đó, chia cả hai vế của phương trình cho 2: x = 6.32 ÷ 2 x = 3.16
Vậy, giá trị của x là 3.16.
c) 64.4x = 168 Để giải phương trình này, ta chia cả hai vế của phương trình cho 64: 4x = 168 ÷ 64 4x = 2.625
Sau đó, chia cả hai vế của phương trình cho 4: x = 2.625 ÷ 4 x = 0.65625
Vậy, giá trị của x là 0.65625.
d) 2x = 16 Để giải phương trình này, ta chia cả hai vế của phương trình cho 2: x = 16 ÷ 2 x = 8 Vậy, giá trị của x là 8.
a, 3\(^x\).3 = 243
3\(^x\) = 243: 3
3\(^x\) = 81
3\(^x\) = 34
\(x\) = 4
b, Giả sử tồn tại \(x\) \(\in\) N* thỏa mãn đề bài ta có:
2\(^x\). 162 = 1024
2\(^x\).81 = 1024 : 2
2\(^x\).81 = 512
2\(x\) = 512 : 81
vì \(x\) \(\in\) N ⇒ 2\(^x\) \(\in\) N ⇒ 512 \(⋮\) 81 ( vô lý)
Vậy điều giả sử là sai Vậy không tồn tại số tự nhiên nào thỏa mãn đề bài
hay \(x\in\) \(\varnothing\)
c, câu c làm tương tự câu b
d, 2\(^x\) = 16
2\(^x\) = 24
\(x\) = 4

Mik chỉ dịch hộ bn thôi còn cách làm thì mình ko bt xl bn nha
Mỗi ô a sẽ tách thành 2 ô b sau 1 phút và mỗi ô b sẽ tách thành 2 ô a sau 2 phút. hiện tại có rất ít ô. sau 10 phút, các nhà khoa học quan sát được 1792 tế bào. lúc đầu có bao nhiêu ô


\(A=\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{2001\cdot2005}\)
\(A=1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-...+\dfrac{1}{2001}-\dfrac{1}{2005}\)
\(A=1-\dfrac{1}{2005}=\dfrac{2004}{2005}\)
\(B=\dfrac{3}{10\cdot12}+\dfrac{3}{12\cdot14}+...+\dfrac{3}{998\cdot1000}\)
\(\dfrac{2}{3}B=\dfrac{2}{10\cdot12}+...+\dfrac{2}{998\cdot1000}\)
\(\dfrac{2}{3}B=\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-...+\dfrac{1}{998}-\dfrac{1}{1000}\)
\(\dfrac{2}{3}B=\dfrac{1}{10}-\dfrac{1}{1000}=\dfrac{99}{1000}\)
\(B=\dfrac{99}{1000}:\dfrac{2}{3}=\dfrac{297}{2000}\)
\(A=\dfrac{4}{1.5}+\dfrac{4}{5.9}+...+\dfrac{4}{2001.2005}\)
\(\Rightarrow A=4\left(\dfrac{1}{1.5}+\dfrac{1}{5.9}+...+\dfrac{1}{2001.2005}\right)\)
\(\Rightarrow A=4.\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{2001}-\dfrac{1}{2005}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2005}\)
\(\Rightarrow A=\dfrac{2004}{2005}\)
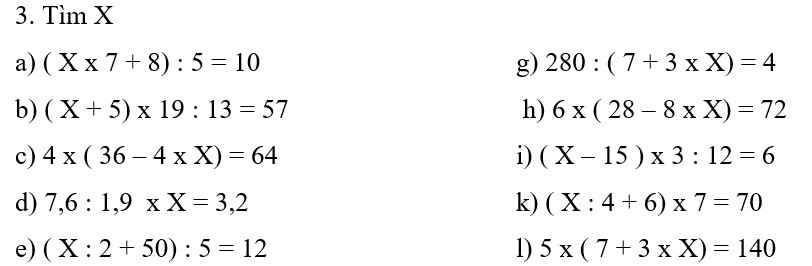

104; 122; 140; 212; 230; 302; 320; 410; 500