Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\sqrt{50}>\sqrt{49}\)
mà \(\sqrt{49}=7\)
nên \(\sqrt{50}>7\)
b: \(\sqrt{27}>\sqrt{25}=5\)
=>\(\dfrac{4}{\sqrt{27}}< \dfrac{4}{5}\)
c: \(\dfrac{3}{\sqrt{7}}>1;\dfrac{\sqrt{7}}{3}< 1\)
Do đó: \(\dfrac{3}{\sqrt{7}}>\dfrac{\sqrt{7}}{3}\)

Bài 2:
a:
\(-4,4\left(9\right)-5,8\left(1\right)\simeq-4,5-5,8=-10,3\)
\(-4,4\left(9\right)-5,8\left(1\right)\)
\(=-\dfrac{9}{2}-\dfrac{-523}{90}=-\dfrac{9}{2}+\dfrac{523}{90}=\dfrac{118}{90}=\dfrac{59}{45}\)
b:
\(-12,\left(7\right)\cdot3,\left(12\right)\simeq-12,8\cdot3,1\simeq-40\)
\(-12,\left(7\right)\cdot3,\left(12\right)\)
\(=-\dfrac{115}{9}\cdot\dfrac{103}{33}=\dfrac{11845}{297}\)
c: \(9,\left(49\right):\left[-5,\left(09\right)\right]\simeq9,5:\left(-5,1\right)\simeq-1,9\)
\(9,\left(49\right):\left[-5,\left(09\right)\right]\)
\(=\dfrac{940}{99}:\dfrac{-56}{11}=\dfrac{940}{99}\cdot\dfrac{11}{-56}\)
\(=\dfrac{940}{-56}\cdot\dfrac{1}{9}=-\dfrac{235}{14\cdot9}=-\dfrac{235}{126}\)
Bài 1:
a: \(9,4\simeq9\)
b: \(3,51\simeq4\)
c: \(-7,505\simeq-8\)
d: \(-1.199\simeq-1\)

Sửa đề: \(\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{2^{12}\cdot9^6+8\cdot9^5}\)
\(=\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^{12}+2^3\cdot3^{10}}\)
\(=\dfrac{2^{12}\cdot3^4\left(3-1\right)}{2^3\cdot3^{10}\left(2^9\cdot3^2+1\right)}\)
\(=\dfrac{2^9}{3^6}\cdot\dfrac{2}{1028\cdot9+1}=\dfrac{2^{10}}{729\left(1028\cdot9+1\right)}\)

\(B=\left(-2\right)+\left(-2\right)^2+...+\left(-2\right)^{2024}\)
=>\(\left(-2\right)\cdot B=\left(-2\right)^2+\left(-2\right)^3+...+\left(-2\right)^{2025}\)
=>\(-2B-B=\left(-2\right)^2+\left(-2\right)^3+...+\left(-2\right)^{2025}-\left(-2\right)-\left(-2\right)^2-...-\left(-2\right)^{2024}\)
=>\(-3B=-2^{2025}+2\)
=>\(B=\dfrac{-2^{2025}+2}{-3}=\dfrac{2^{2025}-2}{3}\)

a: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAHI=ΔAKI
b: ΔAHI=ΔAKI
=>IH=IK
Xét ΔIBC có
IM là đường cao
IM là đường trung tuyến
Do đó: ΔIBC cân tại I
=>IB=IC
Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
IH=IK
Do đó: ΔIHB=ΔIKC
=>BH=CK

Do \(f\left(3\right)=f\left(-3\right)\Rightarrow a.3^2+b.3+c=a.\left(-3\right)^2+b.\left(-3\right)+c\)
\(\Rightarrow9a+3b+c=9a-3b+c\)
\(\Rightarrow6b=0\)
\(\Rightarrow b=0\)
\(\Rightarrow f\left(x\right)=ax^2+c\)
\(f\left(-x\right)=a.\left(-x\right)^2+x=ax^2+c\)
\(\Rightarrow f\left(x\right)=f\left(-x\right)\)

Ta có:
`(25/13)^15 = (25^15)/(13^15) > 1`
`(13/25)^20 = (13^20)/(25^20) < 1`
`-> (13/25)^20 < 1 < (25/13)^15`
Vậy: `(25/13)^15 > (13/25)^20`
(\(\dfrac{25}{13}\))15 > 115 > 1
(\(\dfrac{13}{25}\))20 < 120 < 1
Vậy (\(\dfrac{25}{13}\))15 > (\(\dfrac{13}{25}\))20

a: Ta có: \(\widehat{HAC}+\widehat{ACB}=90^0\)(ΔAHC vuông tại H)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{HAC}=\widehat{ABC}\)
b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)
\(\widehat{CKA}+\widehat{HAK}=90^0\)(ΔHAK vuông tại H)
mà \(\widehat{BAK}=\widehat{HAK}\)(AK là phân giác của góc HAB)
nên \(\widehat{CAK}=\widehat{CKA}\)
c: Xét ΔCAK có \(\widehat{CAK}=\widehat{CKA}\)
nên ΔCAK cân tại C
ΔCAK cân tại C
mà CP là đường phân giác
nên CP\(\perp\)AK

\(\sqrt{x}=2\)
=>\(\left(\sqrt{x}\right)^4=2^4\)
=>\(x^2=16\)
\(\sqrt{x}\) = 2 (\(x\) ≥ 0)
(\(\sqrt{x}\))2 = 22
\(x\) = 4
Thay \(x=4\) vào biểu thức \(x^2\) ta có: \(x^2\) = 42 = 16
Vậy nếu \(\sqrt{x}\) = 2 thì \(x^2\) = 16
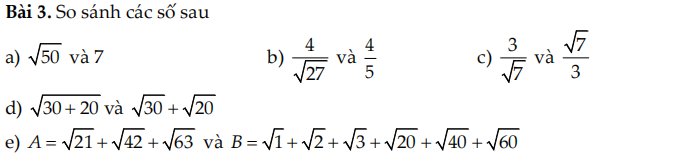


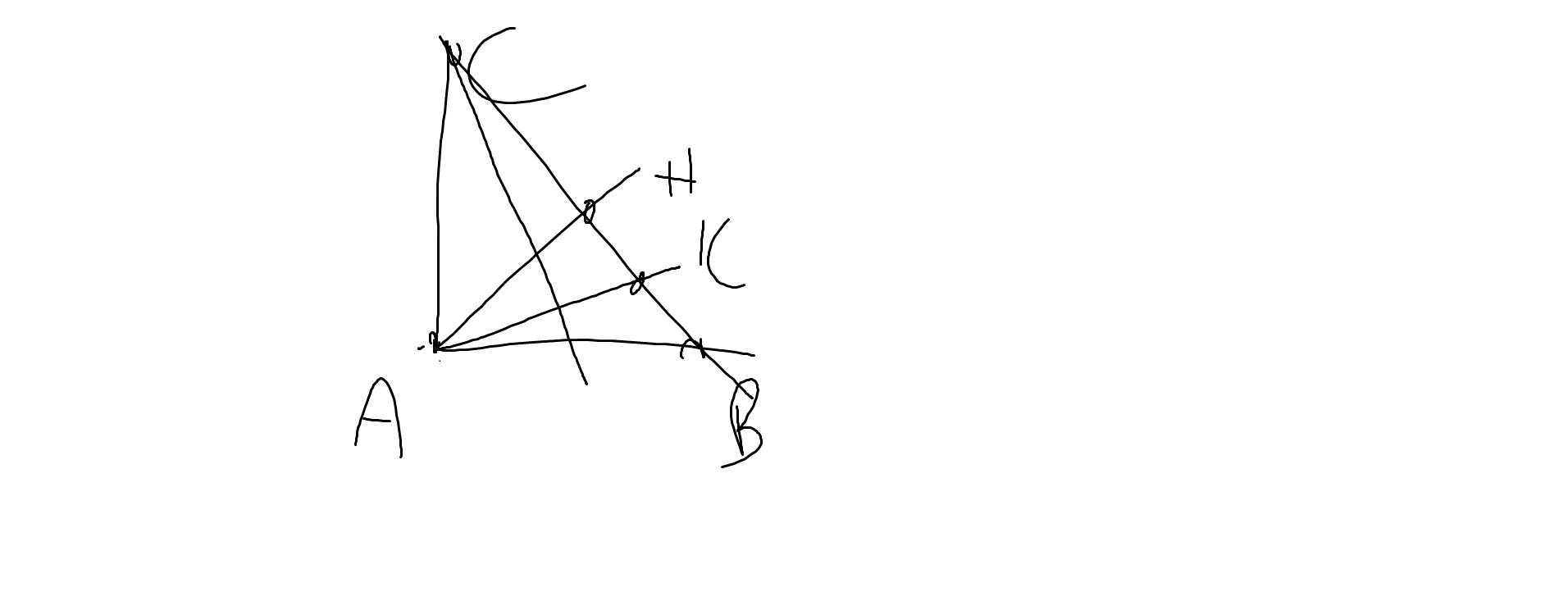
a: \(\left|-\dfrac{1}{3}\right|-\left(-\dfrac{6}{7}\right)^0+\left(\dfrac{1}{2}\right)^2:2\)
\(=\dfrac{1}{3}-1+\dfrac{1}{4}:2=-\dfrac{2}{3}+\dfrac{1}{8}=\dfrac{-16}{24}+\dfrac{3}{24}=-\dfrac{13}{24}\)
b: \(\left(\dfrac{2}{3}\right)^3+\sqrt{\dfrac{49}{81}}-\left|-\dfrac{7}{3}\right|:3\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{3}\cdot\dfrac{1}{3}\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{9}=\dfrac{8}{27}\)
c: \(\sqrt{\dfrac{25}{49}}+\left(5555\right)^0+\left|-\dfrac{2}{7}\right|\)
\(=\dfrac{5}{7}+1+\dfrac{2}{7}\)
=1+1=2