Vi làm 5 tấm thiệp sinh nhật. Biết Vi làm mỗi tấm thiệp như thế hết 4 phút 30 giây. Hỏi Vi làm những tấm thiệp đó trong bao lâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng số viên bi trong hộp là:
56x2=112(viên)
Số viên bi đỏ là \(\dfrac{112+20}{2}=\dfrac{132}{2}=66\left(viên\right)\)
Số viên bi xanh là 66-20=46(viên)
Tổng số viên bi trong hộp là:
56×2=112 (viên)
Số viên bi đỏ là:
(112+20) : 2 =66 ( viên )
Số viên bi xanh là:
66-20=42(viên)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
=>AH là phân giác của góc BAC
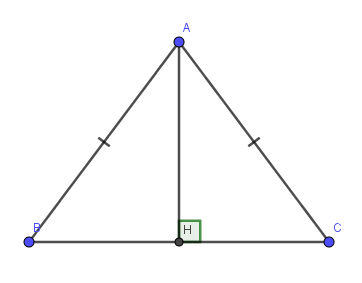
a) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:
\(AB=AC\left(gt\right)\)
\(AH\) là cạnh chung
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)
b) Do \(\Delta AHB=\Delta AHC\left(cmt\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)
\(\Rightarrow AH\) là tia phân giác của \(\widehat{BAC}\)

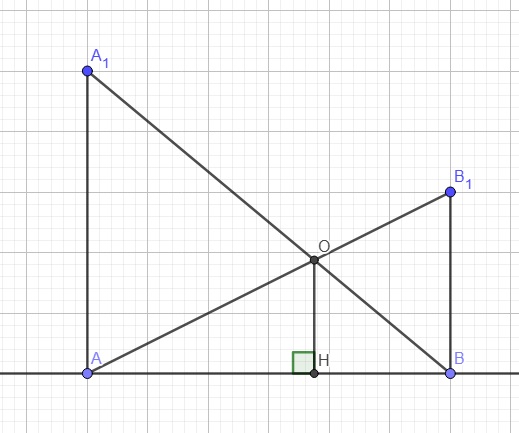
Gọi H là hình chiếu vuông góc của O lên d
\(\Rightarrow AA_1||OH||BB_1\)
Áp dụng định lý Thales trong tam giác \(ABA_1\)
\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)
Áp dụng định lý Thales trong tam giác \(ABB_1\)
\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)
\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)
\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)
\(\Rightarrow OH=\dfrac{a.b}{a+b}\)
Do a, b không đổi \(\Rightarrow OH\) không đổi
Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d

a. Khi gieo con xúc xắc số, các kết quả số chấm xuất hiện có thể là: 1; 2; 3; 4; 5; 6 chấm
Vậy các kết quả có thể để sự kiện số chấm xuất hiện là số nguyên tố xảy ra là:
2, 3, 5 chấm
b. Do 5 khác 6 nên nếu số chấm xuất hiện là 5 thì sự kiện số chấm xuất hiện không phải là 6 có xảy ra.
Các kết quả có thể xảy ra của sự kiện "Số chấm xuất hiện là số nguyên tố"
=>Các kết quả có thể xảy ra là 2;3;5

- Đổi 3dm = 0,3m
- Diện tích một viên gạch là: 0,3m x 0,3m = 0,09m²
- Diện tích căn phòng là: 0,09m² x 200 = 18m²
Đáp số: 18m²
Diện tích của một viên gạch lát nền là:
30×30=900(cm2)
Diện tích căn phòng là:
900×200=180000(cm2)
180000cm2=18m2
Đáp số: 18m2.

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!
đổi 4 phút 30 giấy=4,5 phút
thời gian Vy làm những tấm thiệp là
4,5 phút x 5 = 22,5 phút
đổi 22,5 phút = 22 phút 30 giây
Đáp số 22 phút 30 giây