Tìm n thuộc N để mỗi phép chia sau là phép chia hết
a)\(35x^9y^n:\left(-7x^7y^2\right)\)
b)\(\left(5x^3-7x^2+x\right):3x^n\)
c)\(\left(13x^4y^3-5x^3y^3+6x^2y^2\right):5x^ny^n\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
(a + b)2 - 4ab
= a2 + 2ab + b2 - 4ab
= a2 - 2ab +b2
= (a-b)2 (đpcm)
Bài 2:
\(x^3\) - 9\(x^2\) + 27\(x\) - 27
= (\(x\) - 3)3 (1)
Thay \(x\) = 5 vào (1) ta có: (5-3)3 = 8

\(a,5x\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,3\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow3\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ c,x^2-9x-10=0\\ \Leftrightarrow x^2+x-10x-10=0\\ \Leftrightarrow x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
a, 5\(x\)(\(x^2\) - 9) = 0
\(\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
Vậy \(x\) \(\in\) { -3; 0; 3}
b, 3.(\(x+3\)) - \(x^2\) - 3\(x\) = 0
3.(\(x+3\)) - \(x\).( \(x\) + 3) = 0
(\(x+3\))( 3 - \(x\)) = 0
\(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -3; 3}
c, \(x^2\) - 9\(x\) - 10 = 0
\(x^2\) + \(x\) - 10\(x\) - 10 = 0
\(x.\left(x+1\right)\) - 10.( \(x-1\)) = 0
(\(x+1\))(\(x-10\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -1; 10}

\(a,15x-5xy\\ =5x\left(3-y\right)\\ b,\left(x^2+1\right)^2-4x^2\\ =\left(x^2-x+1\right)\left(x^2+x+1\right)\\ c,x^2-10x-9y^2+25\\ =\left(x-5\right)^2-9y^2\\ =\left(x-9y-5\right)\left(x+9y-5\right)\)

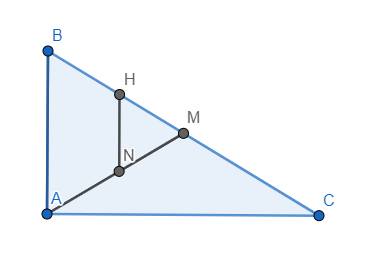
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)

\(\Leftrightarrow4x^2-12x+9+y^2+10y+25=0\)
\(\Leftrightarrow\left(2x-3\right)^2+\left(y+5\right)^2=0\) (1)
Do \(\left(2x-3\right)^2\ge0\) và \(\left(y+5\right)^2\ge0\)
\(\Rightarrow\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)=0\\y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)

\(2x^2-2xy-4x+y^2+4=0\)
\(\Leftrightarrow x^2-2xy+y^2+x^2-4x+4=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2=0\left(1\right)\)
mà \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0,\forall x;y\\\left(x-2\right)^2\ge0,\forall x\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

4\(x^2\) + y2 - 12\(x\) + 10y + 34 = 0
(4\(x^2\) - 12\(x\) + 9) + (y2 + 10y + 25) = 0
(2\(x\) - 3)2 + (y + 5)2 = 0
(2\(x\) - 3)2 ≥ 0 ∀ \(x\); (y + 5)2 ≥ 0 ∀ y
(2\(x-3\))2 + (y + 5)2 = 0 ⇔ \(\left\{{}\begin{matrix}2x-3=0\\y+5=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-5\end{matrix}\right.\)
Kl: (\(x;y\)) = ( \(\dfrac{3}{2}\); -5)
a) \(35x^9y^n=5.\left(7x^9y^n\right)\)
Để \(35x^9y^n⋮\left(-7x^7y^2\right)\)
\(\Rightarrow n\in\left\{0;1;2\right\}\)
b) \(5x^3-7x^2+x=3x\left(\dfrac{5}{3}x^2-\dfrac{7}{3}x+\dfrac{1}{3}\right)\)
Để \(\left(5x^3-7x^2+x\right)⋮3x^n\)
\(\Rightarrow3x\left(\dfrac{5}{3}x^2-\dfrac{7}{3}x+\dfrac{1}{3}\right)⋮3x^n\)
\(\Rightarrow n\in\left\{0;1\right\}\)