Cho tam giác ABC vuông tại A , AB>AC.Tia phân giác góc A cắt BC tại D . Qua D kẻ đường vuông góc với BC tại D , cắt AC tại F . trên AB lấy điểm F sao cho AE=AF. Chứng minh :
a) Góc ABC=góc DEC
b)Tam giác DBF là tam giác cân
c) DB=DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số kẹo ở mỗi gói là `x`:
Số kẹo còn lại sau khi Mai lấy ra là: `8` x `(x - 3) `
Số kẹo còn nguyên ở 5 gói là: `5` x `x`
Mà Mai lấy ra ở mỗi gói 3 cái kẹo còn lại ở 8 gói đúng bằng số kẹo của 5 gói nguyên, nên:
`8` x `(x - 3) = 5` x `x`
`8` x `x - 24 = 5` x `x`
`3` x `x = 24`
`x = 8`
Vậy mỗi gói kẹo có `8` cái
Số kẹo mai có là:
`8 x 8 = 64` (cái)
Đáp số: `64` cái

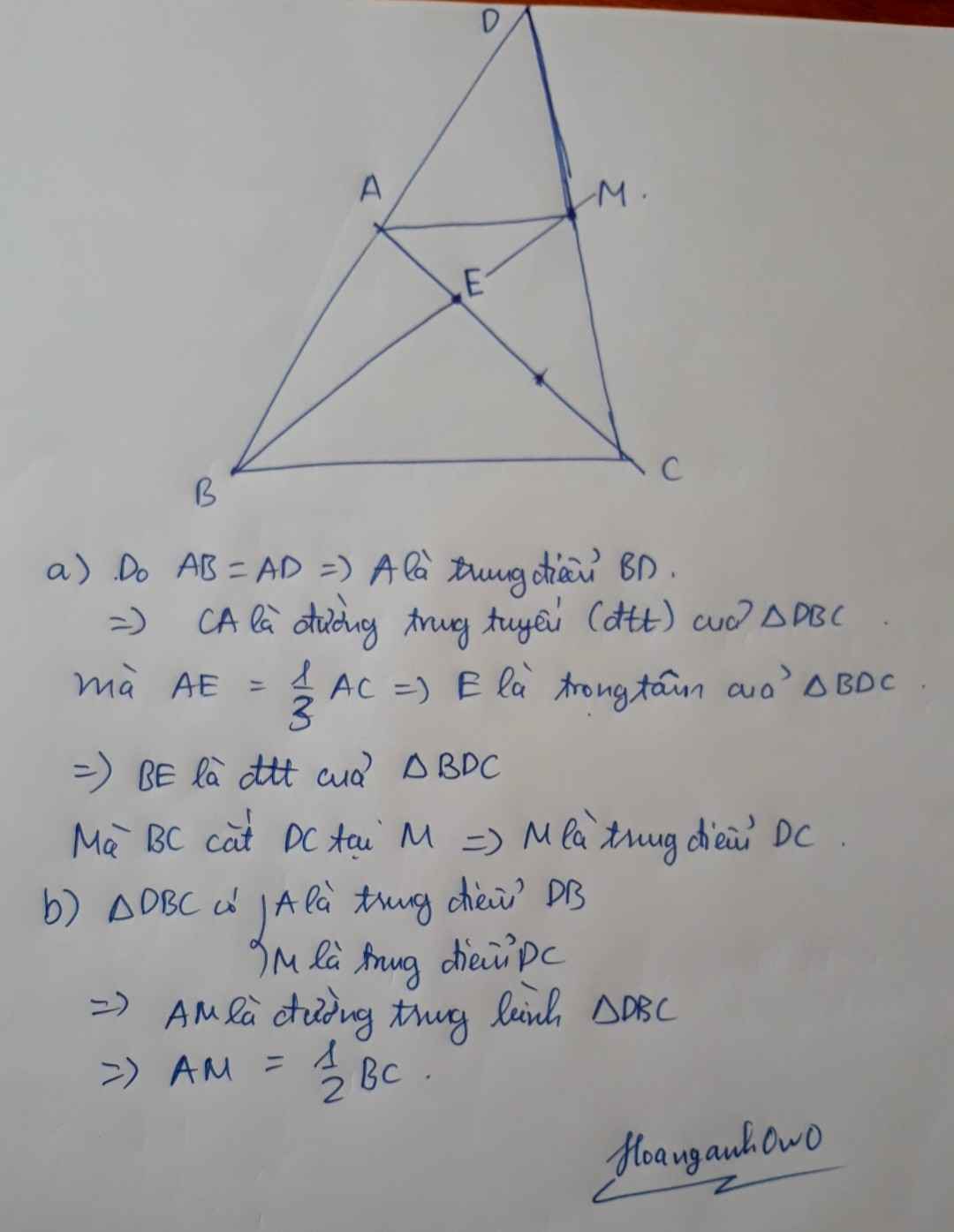
a: Ta có: AB=AD
mà A nằm giữa B và D
nên A là trung điểm của BD
Ta có: \(AE=\dfrac{1}{3}AC\)
=>\(CE=\dfrac{2}{3}CA\)
Xét ΔCBD có
CA là đường trung tuyến
\(CE=\dfrac{2}{3}CA\)
Do đó: E là trọng tâm của ΔBDC
Xét ΔCBD có
E là trọng tâm
M là giao điểm của BE và CD
Do đó: M là trung điểm của CD
b: Xét ΔDBC có
A,M lần lượt là trung điểm của DB,DC
=>AM là đường trung bình của ΔDBC
=>\(AM=\dfrac{1}{2}BC\)
 - Nếu không hiểu thì kết bạn chat riêng để mình hỗ trợ nhé
- Nếu không hiểu thì kết bạn chat riêng để mình hỗ trợ nhé

Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{AB}=\sqrt{3}\)
=>\(\dfrac{AC^2}{AB^2}=3\)
=>\(AC^3=3AB^2\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(4\cdot AB^2=2^2=4\)
=>\(AB^2=1\)
=>AB=1(cm)
=>\(AC=1\cdot\sqrt{3}=\sqrt{3}\left(cm\right)\)

Kẻ IM\(\perp\)BC tại M
Xét ΔBHI vuông tại H và ΔBMI vuông tại M có
BI chung
\(\widehat{HBI}=\widehat{MBI}\)
Do đó: ΔBHI=ΔBMI
=>IH=IM
Xét ΔIMC vuông tại M và ΔIKC vuông tại K có
CI chung
\(\widehat{ICM}=\widehat{ICK}\)
Do đó: ΔIMC=ΔIKC
=>IM=IK
=>IH=IK
Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
IH=IK
Do đó: ΔAHI=ΔAKI
=>\(\widehat{HAI}=\widehat{KAI}\)
=>AI là phân giác của góc BAC

\(\dfrac{24}{18}=\dfrac{24:6}{18:6}=\dfrac{4}{3}=\dfrac{4\times\dfrac{100}{3}}{3\times\dfrac{100}{3}}=\dfrac{\dfrac{400}{3}}{100}\)
\(\dfrac{24}{18}=\dfrac{4}{3}\)
Phân số thập phân là phân số có thể viết được dưới dạng phân số có mẫu là các số như `10;100;1000;...` (các số chia hết cho `10`)
Mà các số `10,100,1000,...`. thì không chia hết cho `3` (do tổng các chữ số chỉ bằng `1`)
Nên phân số \(\dfrac{4}{3}\) không thể viết được dưới dạng phân số thập phân


Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{AC}{15}=\dfrac{3}{5}\)
=>\(AC=15\cdot\dfrac{3}{5}=9\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB=\sqrt{15^2-9^2}=12\left(cm\right)\)
Tam giác `ABC` vuông tại `A`
`=> AC = BC . sinB = 15 . 3/5 = 9 (cm)`
Và `AB =` \(\sqrt{BC^2-AC^2}=\sqrt{15^2-9^2}=\sqrt{144}=12\) `(cm)`

Điều kiện \(\overline{9,2x8}\)\(>\)\(92,78\) do đó \(x\)có 1 chữ số
\(\Rightarrow x\)\(=\)\(8;9\)
Thay vào ta đc:\(9,288;9,298\)
Vậy \(x\)\(=\)\(8;9\)
ab<ac nhé nhầm thành ab>ac