Bài 1;

a: ABCD là hình thang cân

=>\(\widehat{D}=\widehat{C}=60^0\)

ABCD là hình thang

=>\(\widehat{BAD}+\widehat{ADC}=180^0\)

=>\(\widehat{BAD}=120^0\)

ABCD là hình thang cân

=>\(\widehat{BAD}=\widehat{ABC}\)

=>\(\widehat{ABC}=120^0\)

b: Xét ΔAED vuông tại E và ΔBFC vuông tại F có

AD=BC

\(\widehat{ADE}=\widehat{BCF}\)

Do đó: ΔAED=ΔBFC

=>AE=BF

Bài 4:

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có

AB=AC

\(\widehat{BAH}\) chung

Do đó: ΔAHB=ΔAKC

b: ΔAHB=ΔAKC

=>BH=CK

Xét ΔKBC vuông tại K và ΔHCB vuông tại H có

BC chung

KC=HB

Do đó: ΔKBC=ΔHCB

c: ΔAHB=ΔAKC

=>AH=AK

Xét ΔABC có \(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)

nên KH//BC

Xét tứ giác BKHC có KH//BC và BH=KC

nên BKHC là hình thang cân

Sao dấu + với dấu - lại ở ngay cạnh nhau được bạn nhỉ? Hay ý bạn là: 

\(\dfrac{7}{21}+\dfrac{-21}{7}\) 

Lần sau bạn bấm vài biểu tượng Σ để nhập các công thức toán học nhé!

\(\dfrac{15}{34}+\dfrac{15}{17}+\dfrac{19}{34}-1\dfrac{15}{17}+\dfrac{2}{3}\)

\(=\dfrac{15}{34}+\dfrac{19}{34}+\dfrac{15}{17}-1-\dfrac{15}{17}+\dfrac{2}{3}\)

\(=1-1+\dfrac{2}{3}=\dfrac{2}{3}\)

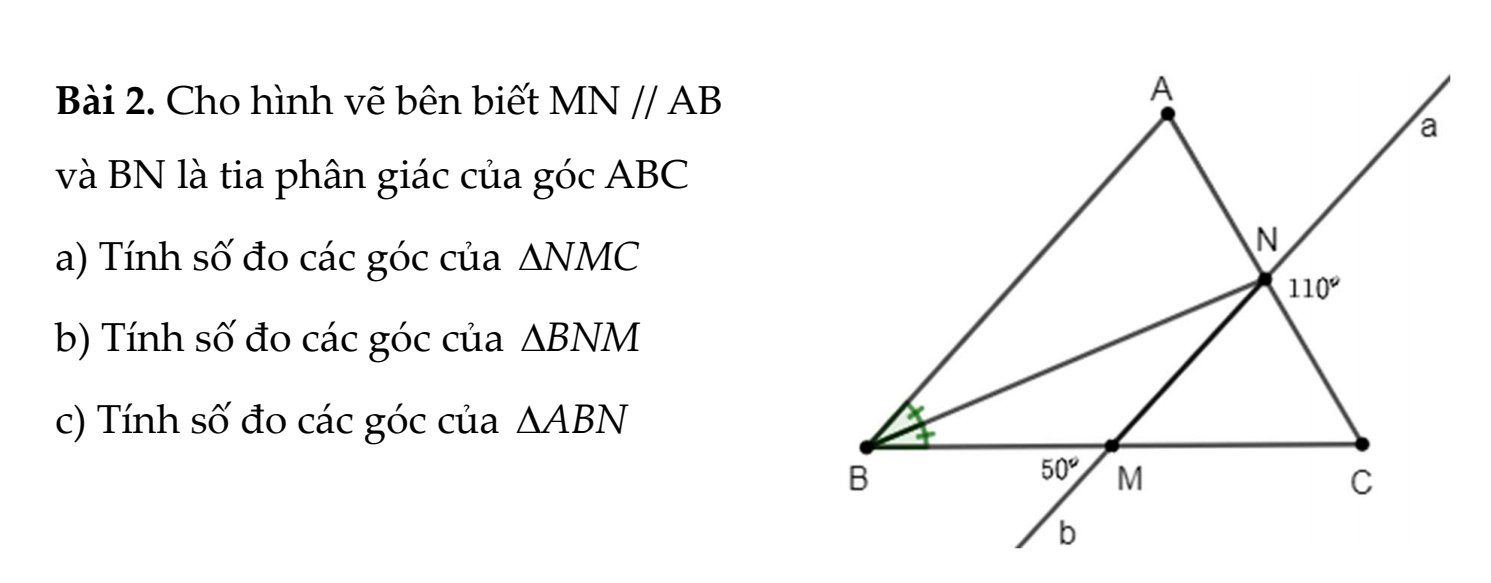
a: Ta có: \(\widehat{bMB}=\widehat{NMC}\)(hai góc đối đỉnh)

mà \(\widehat{bMB}=50^0\)

nên \(\widehat{NMC}=50^0\)

Ta có: \(\widehat{MNC}+\widehat{aNC}=180^0\)(hai góc kề bù)

=>\(\widehat{MNC}+110^0=180^0\)

=>\(\widehat{MNC}=70^0\)

Xét ΔMNC có \(\widehat{NMC}+\widehat{MNC}+\widehat{C}=180^0\)

=>\(\widehat{C}+50^0+70^0=180^0\)

=>\(\widehat{C}=60^0\)

b: Ta có: \(\widehat{NMB}+\widehat{NMC}=180^0\)(hai góc kề bù)

=>\(\widehat{NMB}+50^0=180^0\)

=>\(\widehat{NMB}=130^0\)

Ta có: MN//AB

=>\(\widehat{CMN}=\widehat{CBA}\)(hai góc đồng vị)

=>\(\widehat{CBA}=50^0\)

BN là phân giác của góc CBA

=>\(\widehat{NBM}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔNMB có \(\widehat{NMB}+\widehat{BNM}+\widehat{NBM}=180^0\)

=>\(\widehat{MNB}=180^0-130^0-25^0=25^0\)

c: BN là phân giác của góc CBA

=>\(\widehat{ABN}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

=>\(\widehat{BAN}+60^0+50^0=180^0\)

=>\(\widehat{BAN}=70^0\)

Xét ΔBAN có \(\widehat{BAN}+\widehat{ABN}+\widehat{ANB}=180^0\)

=>\(\widehat{ANB}=180^0-75^0-25^0=85^0\)

Bài 4: \(8^{10}\cdot125^{10}< =2^n\cdot5^n< =20^{16}\cdot5^{16}\)

=>\(1000^{10}< =10^n< =100^{16}\)

=>\(10^{30}< =10^n< =10^{32}\)

=>30<=n<=32

mà n là số tự nhiên

nên \(n\in\left\{30;31;32\right\}\)

Bài 1:

1: \(3^{-2}\cdot3^4\cdot3^n=3^7\)

=>\(3^n\cdot3^2=3^7\)

=>n+2=7

=>n=7-2=5

2: \(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)

=>\(2^n\left(\dfrac{1}{2}+4\right)=2^5\cdot9\)

=>\(2^n=9\cdot2^5:\dfrac{9}{2}=2^6\)

=>n=6

Bài 2:

1: \(243>=3^n>=9\)

=>\(3^2< =3^n< =3^5\)

=>2<=n<=5

mà n là số tự nhiên

nên \(n\in\left\{2;3;4;5\right\}\)

2: \(2^{n+3}\cdot2^n=144\)

=>\(2^{2n+3}=144\)

=>\(2n+3=log_2144\)

=>\(2n=log_2144-3\)

=>\(n=\dfrac{log_2144-3}{2}\left(loại\right)\)

Bài 3:

\(10^x:5^y=20^y\)

=>\(10^x=20^y\cdot5^y=100^y=10^{2y}\)

=>x=2y

vậy: \(\left(x;y\right)\in\){(2k;k)|\(k\in N\)}

a: Ta có: \(\widehat{ICA}+\widehat{ICB}=\widehat{ACB}=90^0\)

\(\widehat{ICB}+\widehat{NCB}=\widehat{NCI}=90^0\)

Do đó: \(\widehat{ICA}=\widehat{NCB}\)

Ta có: \(\widehat{CAI}+\widehat{CBI}=90^0\)(ΔCBA vuông tại C)

\(\widehat{CBI}+\widehat{CBN}=\widehat{NBI}=90^0\)

Do đó: \(\widehat{CAI}=\widehat{CBN}\)

Xét ΔCAI và ΔCBN có

\(\widehat{CAI}=\widehat{CBN}\)

\(\widehat{ICA}=\widehat{NCB}\)

Do đó: ΔCAI~ΔCBN

b: Ta có: \(\widehat{ACM}+\widehat{ACI}=\widehat{ICM}=90^0\)

\(\widehat{ICA}+\widehat{ICB}=\widehat{ACB}=90^0\)

Do đó: \(\widehat{ACM}=\widehat{ICB}\)

Ta có: \(\widehat{CAM}+\widehat{CAB}=\widehat{BAM}=90^0\)

\(\widehat{CAB}+\widehat{CBA}=90^0\)(ΔCAB vuông tại C)

Do đó: \(\widehat{CAM}=\widehat{CBA}\)

Xét ΔCAM và ΔCBI có

\(\widehat{CAM}=\widehat{CBI}\)

\(\widehat{ACM}=\widehat{BCI}\)

Do đó: ΔCAM~ΔCBI

=>\(\dfrac{AC}{CB}=\dfrac{AM}{BI}\)

=>\(AC\cdot BI=MA\cdot BC\)

c: Xét tứ giác CIBN có \(\widehat{ICN}+\widehat{IBN}=90^0+90^0=180^0\)

nên CIBN là tứ giác nội tiếp

=>\(\widehat{CIN}=\widehat{CBN}\)

=>\(\widehat{CIN}=\widehat{BAC}\)

a: \(\left(x+2\right)^2-\left(x-2\right)\left(x+1\right)=3\)

=>\(x^2+4x+4-\left(x^2-x-2\right)=3\)

=>\(x^2+4x+4-x^2+x+2-3=0\)

=>5x+3=0

=>5x=-3

=>\(x=-\dfrac{3}{5}\)

b: \(\left(2x+3\right)^2-4\left(x-1\right)^2=0\)

=>\(\left(2x+3\right)^2-\left(2x-2\right)^2=0\)

=>\(\left(2x+3+2x-2\right)\left(2x+3-2x+2\right)=0\)

=>\(5\left(4x+1\right)=0\)

=>4x+1=0

=>4x=-1

=>\(x=-\dfrac{1}{4}\)

c: \(\left(x+1\right)\left(x^2-x+1\right)-x\left(x^2+2\right)-2=0\)

=>\(x^3+1-x^3-2x-2=0\)

=>-2x-1=0

=>-2x=1

=>\(x=\dfrac{1}{-2}=-\dfrac{1}{2}\)

b: Chọn mp(SAC) có chứa SC

\(I\in SA\subset\left(SAC\right);I\in\left(BIK\right)\)

Do đó: \(I\in\left(SAC\right)\cap\left(BIK\right)\)

Trong mp(ABCD), gọi H là giao điểm của AC và BK

=>\(H\in\left(SAC\right)\cap\left(BIK\right)\)

=>\(\left(SAC\right)\cap\left(BIK\right)=HI\)

Gọi M là giao điểm của HI với SC

=>M là giao điểm của SC với mp(BIK)

Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\)

Nếu thêm 2 đơn vị vào tử số thì phân số mới có giá trị bằng 1 nên \(\dfrac{a+2}{b}=1\)

=>a+2=b

=>b=a+2

Nếu chuyển 5 đơn vị từ tử số xuống phân số thì phân số mới có giá trị là 1/2 nên \(\dfrac{a-5}{b+5}=\dfrac{1}{2}\)

=>2(a-5)=b+5

=>2a-10=a+7

=>2a-a=10+7

=>a=17

=>b=17+2=19

vậy: Phân số cần tìm là \(\dfrac{17}{19}\)