kẻ CM//a và DN//bB(CM và Aa nằm cùng phía với nửa mặt phẳng chứa tia AC, DN và Bb nằm khác phía với nửa mặt phẳng chứa tia DB

CM//Aa

=>\(\widehat{MCA}=\widehat{A_1}\)

Ta có: CM//a

DN//b

mà a//b

nên CM//DN//a//b

CM//DN

=>\(\widehat{MCD}=\widehat{CDN}\)

DN//Bb

=>\(\widehat{NDB}=\widehat{B_1}\)

Ta có: \(\widehat{ACD}=\widehat{ACM}+\widehat{CDM}=\widehat{CDN}+\widehat{B_1}\)

\(\widehat{CDB}=\widehat{CDN}+\widehat{NDB}=\widehat{CDN}+\widehat{B_1}\)

Do đó: \(\widehat{ACD}=\widehat{CDB}\)

\(2n-1⋮2n+3\)

=>\(2n+3-4⋮2n+3\)

=>\(-4⋮2n+3\)

=>\(2n+3\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(2n\in\left\{-2;-4;-1;-5;1;-7\right\}\)

=>\(n\in\left\{-1;-2;-\dfrac{1}{2};-\dfrac{5}{2};\dfrac{1}{2};-\dfrac{7}{2}\right\}\)

\(2n+1⋮n+5\)

=>\(2n+10-9⋮n+5\)

=>\(-9⋮n+5\)

=>\(n+5\in\left\{1;-1;3;-3;9;-9\right\}\)

=>\(n\in\left\{-4;-6;-2;-8;4;-14\right\}\)

Bài 2:

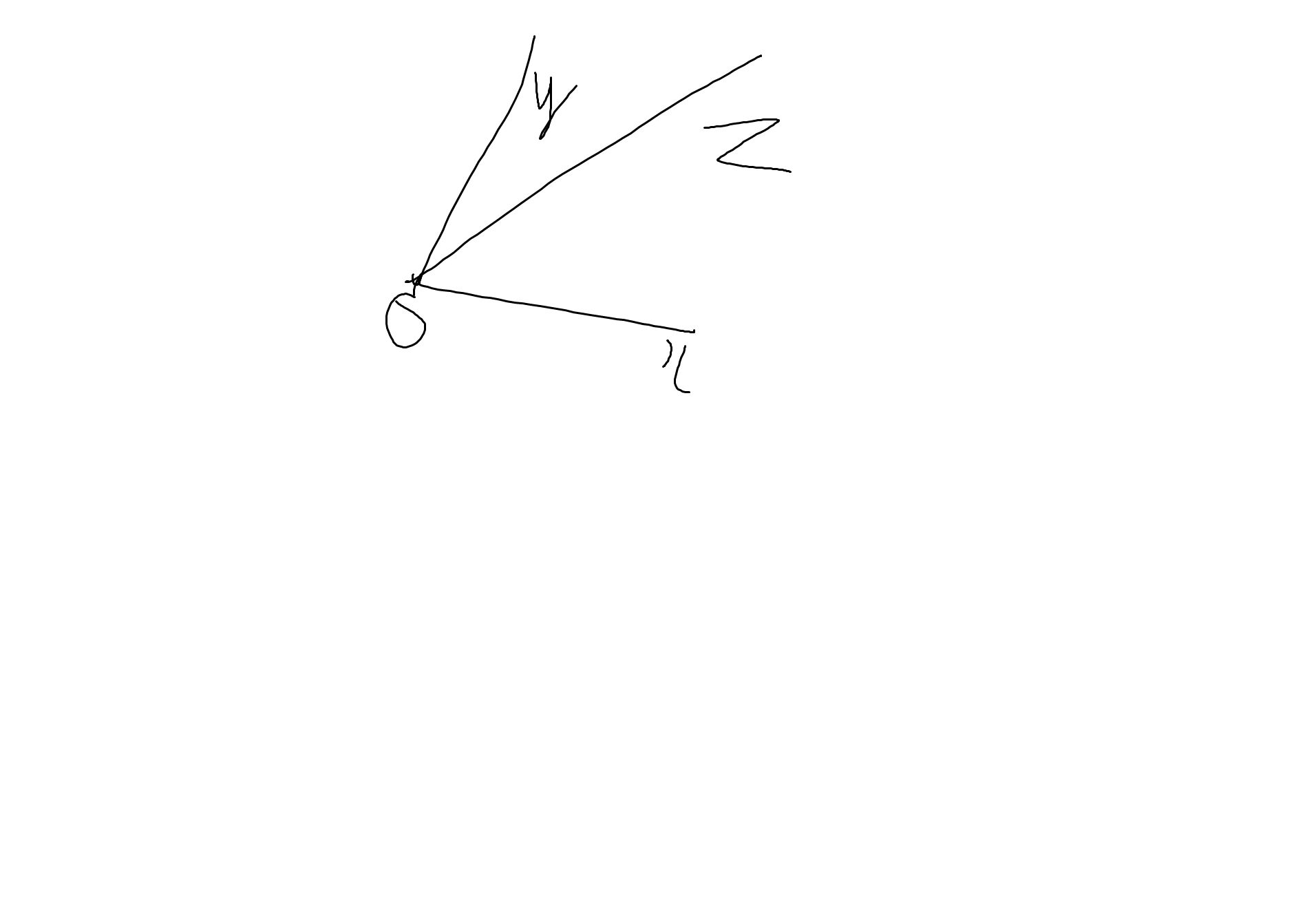
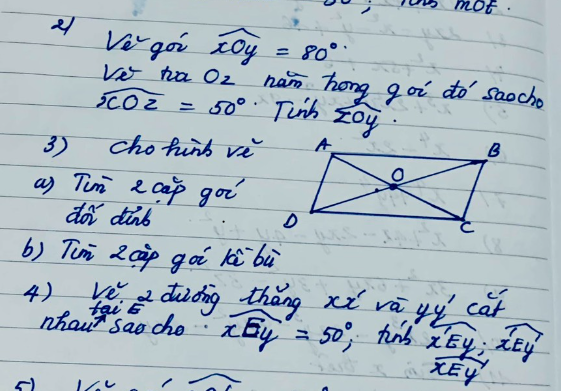
Vì \(\widehat{xOz}< \widehat{xOy}\left(50^0< 80^0\right)\)

nên tia Oz nằm giữa hai tia Ox,Oy

=>\(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)

=>\(\widehat{yOz}=80^0-50^0=30^0\)

Bài 4:

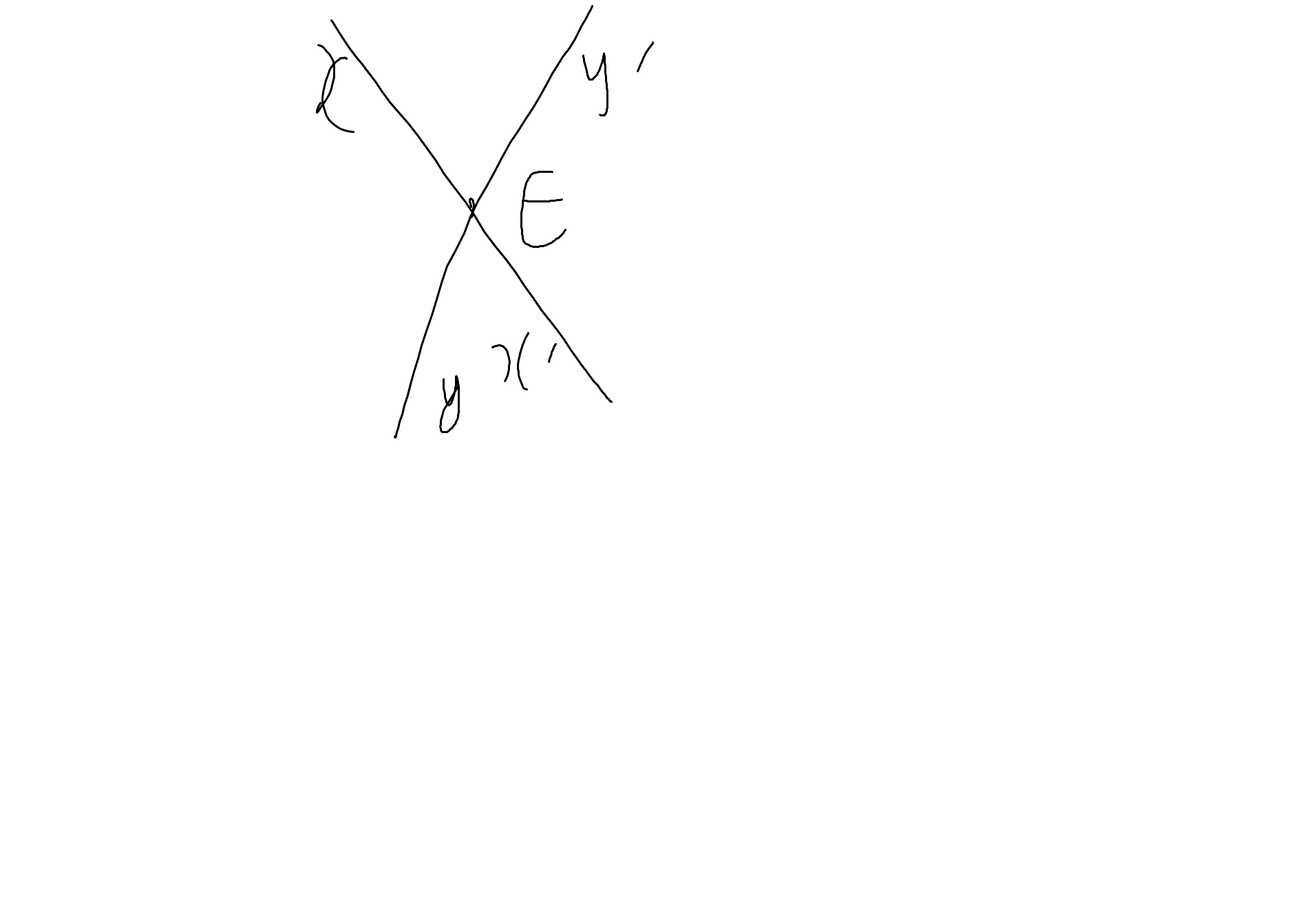
Ta có: \(\widehat{xEy}+\widehat{xEy'}=180^0\)(hai góc kề bù)

=>\(\widehat{xEy'}=180^0-50^0=130^0\)

Ta có: \(\widehat{xEy}=\widehat{x'Ey'}\)(hai góc đối đỉnh)

mà \(\widehat{xEy}=50^0\)

nên \(\widehat{x'Ey'}=50^0\)

Ta có: \(\widehat{xEy'}=\widehat{x'Ey}\)(hai góc đối đỉnh)

mà \(\widehat{xEy'}=130^0\)

nên \(\widehat{x'Ey}=130^0\)

Ta có:

\(-x^2+x-5\\ =-x^2+x-\dfrac{1}{4}+\dfrac{1}{4}-5\\ =-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}-5\\ =-\left[x^2-2.\dfrac{1}{2}.x+\left(\dfrac{1}{2}\right)^2\right]-\dfrac{19}{4}\\ =-\left(x-\dfrac{1}{2}\right)^2-\dfrac{19}{4}\)

Nhận xét:

\(\left(x-\dfrac{1}{2}\right)^2\ge0,\forall x\\ \Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0,\forall x\\ \Rightarrow-\left(x-\dfrac{1}{2}\right)^2-\dfrac{19}{4}\le-\dfrac{19}{4},\forall x\)
hay \(-x^2+x-5\le-\dfrac{19}{4},\forall x\) 
Dấu "=" xảy ra khi và chỉ khi:
\(x-\dfrac{1}{2}\\=0\\ \Rightarrow x=\dfrac{1}{2}\)  
Vậy...

\(\left|x-2\right|>=0\forall x\)

\(\left|2x+y-z\right|>=0\forall x,y,z\)

\(\left|2z+1\right|>=0\forall z\)

Do đó: \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|>=0\forall x,y,z\)

mà \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|< =0\)

nên Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\2x+y-z=0\\2z+1=0\\\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\z=-\dfrac{1}{2}\\y=-2x+z=-2\cdot2+\dfrac{-1}{2}=-4-\dfrac{1}{2}=-\dfrac{9}{2}\end{matrix}\right.\)

\(372-19\cdot4+981:19-13\)

=372-76+981/19-13

\(=283+\dfrac{981}{19}=\dfrac{6358}{19}\)

Bạn làm 2 Trg họp thôi
x- 15= 0 x =15
2x-16=0 x=8

ta có 2 trương hợp

th1 x-15 =0

x=0+15

x=15

th2

2x-16=0

2x=16

x=8

Gọi vận tốc của người thứ hai là x(km/h)

(Điều kiện: x>0)

vận tốc của người thứ nhất là x+4(km/h)

Thời gian người thứ nhất đi từ A đến B là \(\dfrac{24}{x+4}\left(giờ\right)\)

Thời gian người thứ hai đi từ A đến B là \(\dfrac{24}{x}\left(giờ\right)\)

Người thứ nhất đến sớm hơn người thứ hai 30p=0,5 giờ nên ta có:

\(\dfrac{24}{x}-\dfrac{24}{x+4}=0,5\)

=>\(\dfrac{48}{x}-\dfrac{48}{x+4}=1\)

=>\(\dfrac{48x+192-48x}{x^2+4x}=1\)

=>\(x^2+4x=192\)

=>\(x^2+4x-192=0\)

=>(x+16)(x-12)=0

=>\(\left[{}\begin{matrix}x=-16\left(loại\right)\\x=12\left(nhận\right)\end{matrix}\right.\)

Vậy: vận tốc của người thứ hai là 12km/h

vận tốc của người thứ nhất là 12+4=16km/h