tìm x thuộc Q biết: 30(x-7/12)-24x=100+6(x-3/4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(x-3)(x+4) > 0`
`=> x - 3` và `x + 4` cùng dấu
Trường hợp 1: `{(x-3>0),(x+4>0):}`
`=> {(x>3),(x>-4):}`
`=> x > 3`
Trường hợp 2: `{(x-3<0),(x+4<0):}`
`=> {(x<3),(x<-4):}`
`=> x < -4`
Vậy ...
a; (\(x-3\))(\(x+4\)) > 0
\(x-3=0\) ⇒ \(x=3\)
\(x+4\) = 0 ⇒ \(x=-4\)
Lập bảng ta có:
| \(x\) | - 4 3 |
| \(x-3\) | - - 0 + |
| \(x+4\) | - 0 + + |
| (\(x-3\))(\(x+4\)) | + 0 - 0 + |
Theo bảng trên ta có:
\(x\) \(\in\) (- ∞; -4) \(\cup\)(3 ; + ∞)

\(\dfrac{x}{y}\) = 5,4 và \(\dfrac{x}{y^2}\) = 6 (y ≠ 0)
(\(\dfrac{x}{y}\)) = 5,42 ⇒ \(\left(\dfrac{x}{y}\right)^2\)= 29,16;
Thay \(\dfrac{x}{y^2}\) = 6 vào biểu thức (\(\dfrac{x}{y}\))2 = 29,16 ta được:
\(x.\)6 = 29,16 ⇒ \(x=\) 29,16 : 6 ⇒ \(x\) = 4,86
Thay \(x=4,86\) vào biểu thức \(\dfrac{x}{y}\) = 5,4 ta được
\(4,86\) : y = 5,4 ⇒ y = 4,86 : 5,4 ⇒ y = 0,9
Vậy (\(x;y\)) = (4,86; 0,9)

a \(\in\) Z; b \(\in\) n*; n \(\in\) N* a < b
Ta có: \(\dfrac{a}{b}\) = 1 - \(\dfrac{b-a}{b}\)
\(\dfrac{a+n}{b+n}\) = 1 - \(\dfrac{b-a}{b+n}\)
Vì b > a nên b - a > 0, mà n; b \(\in\) N* nên
\(\dfrac{b-a}{b}\) > 0; \(\dfrac{b-a}{b+n}\) > 0
⇒ \(\dfrac{b-a}{b}\) > \(\dfrac{b-a}{b+n}\)
⇒ \(\dfrac{a}{b}\) < \(\dfrac{a+n}{b+n}\)
b; Vì a > b mà b \(\in\) N* nên a \(\in\) Z+
\(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b}\)
\(\dfrac{a+n}{b+n}\) = 1 + \(\dfrac{a-b}{b+n}\)
Vì a > b mà a \(\in\) Z+ nên a - b > 0
Mặt khác: b; n \(\in\) N* nên \(\dfrac{a-b}{b}\); \(\dfrac{a-b}{b+n}\) > 0
⇒ \(\dfrac{a-b}{b}\) > \(\dfrac{a-b}{a+n}\) (hai phân số dương có cùng tử số, phân số nào có mẫu lớn hơn thì phân số đó nhỏ hơn và ngược lại)
⇒ \(\dfrac{a}{b}\) > \(\dfrac{a+n}{b+n}\) (Hai phân số phân số nào có phần hơn lớn hơn thì phân só đó lớn hơn)

`((-27)^10 . 16^25)/(6^30 . (-32)^15)`
`= (3^30 . 2^100)/(2^30 . 3^30 . -2^75)`
`= (2^100)/(2^30 . -2^75)`
`= (2^70)/(-2^75)`
`= -2^145`
A = \(\dfrac{\left(-27\right)^{10}.16^{25}}{6^{30}.\left(-32\right)^{15}}\)
A = \(\dfrac{\left(3^3\right)^{10}.\left(2^4\right)^{25}}{\left(2.3\right)^{30}.\left(-32\right)^{15}}\)
A = \(\dfrac{3^{30}.2^{100}}{2^{30}.3^{30}.\left(-2^5\right)^{15}}\)
A = \(\dfrac{3^{20}.2^{100}}{3^{30}[2^{30}.\left(-2\right)^{75}].}\)
A = \(-\dfrac{2^{100}}{\left[2^{30}.\left(2\right)^{75}\right]}\)
A = -2100 - 30 - 75
A = - 270-75
A = -2-5
A = - \(\dfrac{1}{32}\)

\(\left(x+\dfrac{1}{3}\right)^3=\left(\dfrac{2}{3}\right)^6\\ \Rightarrow\left(x+\dfrac{1}{3}\right)^3=\left[\left(\dfrac{2}{3}\right)^2\right]^3\\ \Rightarrow\left(x+\dfrac{1}{3}\right)^3=\left(\dfrac{4}{9}\right)^3\\ \Rightarrow x+\dfrac{1}{3}=\dfrac{4}{9}\\ \Rightarrow x=\dfrac{4}{9}-\dfrac{1}{3}\\ \Rightarrow x=\dfrac{4}{9}-\dfrac{3}{9}\\ \Rightarrow x=\dfrac{1}{9}\)

`#3107.101107`
\(\left(x+\dfrac{1}{3}\right)^2=\left(\pm\dfrac{2}{3}\right)^6\\ \left(x+\dfrac{1}{3}\right)^2=\left[\pm\left(\dfrac{2}{3}\right)^3\right]^2\\ \left(x+\dfrac{1}{3}\right)^2=\left(\pm\dfrac{8}{27}\right)^2\)
TH1: \(x+\dfrac{1}{3}=\dfrac{8}{27}\\ x=\dfrac{8}{27}-\dfrac{1}{3}\\ x=-\dfrac{1}{27}\)
TH2:
\(x+\dfrac{1}{3}=-\dfrac{8}{27}\\ x=-\dfrac{8}{27}-\dfrac{1}{3}\\ x=-\dfrac{17}{27}\)
Vậy, `x \in {-1/27; -17/27}.`

\(\dfrac{x}{8}=\dfrac{y}{-7}=\dfrac{z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x}{8}=\dfrac{y}{-7}=\dfrac{z}{12}=\dfrac{-3x+10y-2z}{-24-70-24}=\dfrac{236}{-118}=-2\)
Do đó
\(x=\left(-2\right)\times8=-16\)
\(y=\left(-2\right)\times\left(-7\right)=14\)
\(z=\left(-2\right)\times12=-24\)
Vậy x = -16 ; y = 14 ; z = -24
TTôi nghe nói Trong "Principia Mathematica" của Bertrand Russell và Alfred North Whitehead, việc chứng minh 1 + 1 = 2 mất khoảng 362 trang. Đây là một phần của nỗ lực xây dựng toán học dựa trên logic hình thức. Chứng minh này phản ánh sự phức tạp của các định nghĩa và tiên đề trong lý thuyết tập hợp và số học. Nếu bạn cần thêm thông tin về nội dung cụ thể, hãy cho tôi biết! Chứng minh 1 + 1 = 2 trong "Principia Mathematica" được xem là khó khăn vì nó yêu cầu hiểu biết sâu sắc về logic hình thức và các định nghĩa phức tạp. Mặc dù kết quả cuối cùng có vẻ đơn giản, quá trình chứng minh đòi hỏi nhiều bước logic và khái niệm toán học. Nếu bạn không quen với lý thuyết này, nó có thể khá trừu tượng và khó tiếp cận.

\(2a-b=\dfrac{2}{3}\left(a+b\right)\)
\(3\left(2a-b\right)=2\left(a+b\right)\)
\(6a-3b=2a+2b\)
\(4a=5b\)
\(a=\dfrac{5}{4}b\)
Thay vào A ta được:
\(A=\dfrac{\left(\dfrac{5}{4}b\right)^4+5^4}{b^4+4^4}=\dfrac{\dfrac{5^4}{4^4}\left(b^4+4^4\right)}{b^4+4}=\dfrac{5^4}{4^4}\)

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\)
\(\dfrac{x+y}{xy}=\dfrac{1}{3}\)
\(3\left(x+y\right)=xy\)
\(xy-3x-3y=0\)
\(xy-3x-3y+9=9\)
\(x\left(y-3\right)-3\left(y-3\right)=9\)
\(\left(x-3\right)\left(y-3\right)=9\)
Ta có bảng sau:
| x-3 | -9 | -3 | -1 | 1 | 3 | 9 |
| y-3 | -1 | -3 | -9 | 9 | 3 | 1 |
| x | -6 | 0 (loại) | 2 | 4 | 6 | 12 |
| y | 2 | 0 (loại) | -6 | 12 | 6 | 4 |
Vậy \(\left(x;y\right)=\left(-6;2\right);\left(2;-6\right);\left(4;12\right);\left(6;6\right);\left(12;4\right)\)
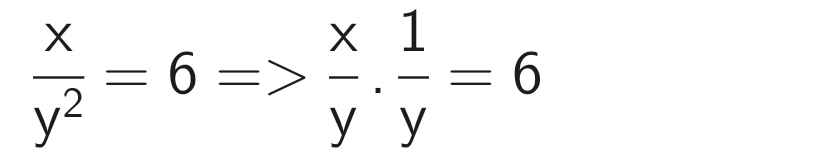
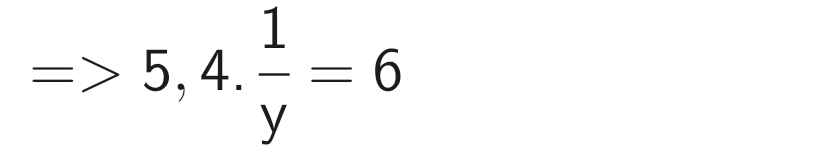
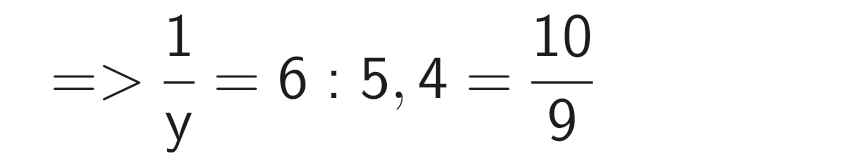
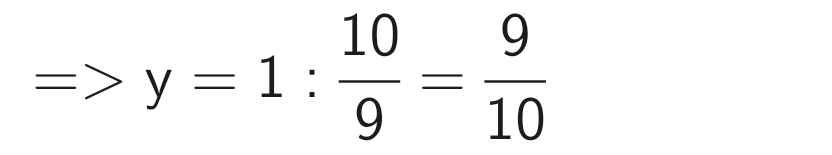

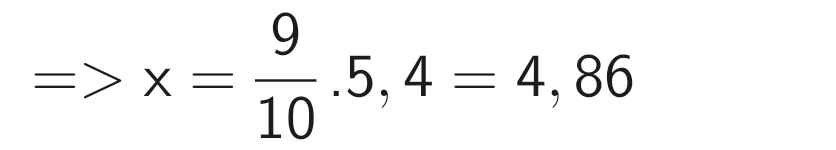
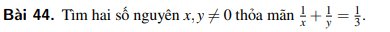
30.(\(x-\dfrac{7}{12}\)) - 24\(x\) = 100 + 6.(\(x\) - \(\dfrac{3}{4}\))
30\(x\) - \(\dfrac{35}{2}\) - 24\(x\) = 100 + 6\(x\) - \(\dfrac{9}{2}\)
30\(x\) - 24\(x\) - 6\(x\) = 100 - \(\dfrac{9}{2}\) + \(\dfrac{35}{2}\)
6\(x\) - 6\(x\) = 100 - (\(\dfrac{9}{2}\) - \(\dfrac{35}{2}\))
0 = 100 + 13
0 = 113 (vô lý)
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài.