Xét ΔOAD và ΔOBC có

OA=OB

\(\widehat{AOD}\) chung

OD=OC

Do đó: ΔOAD=ΔOBC

=>AD=BC

a: Xét ΔABD vuông tại A và ΔABC vuông tại A có

AB chung

AD=AC

Do đó: ΔABD=ΔABC

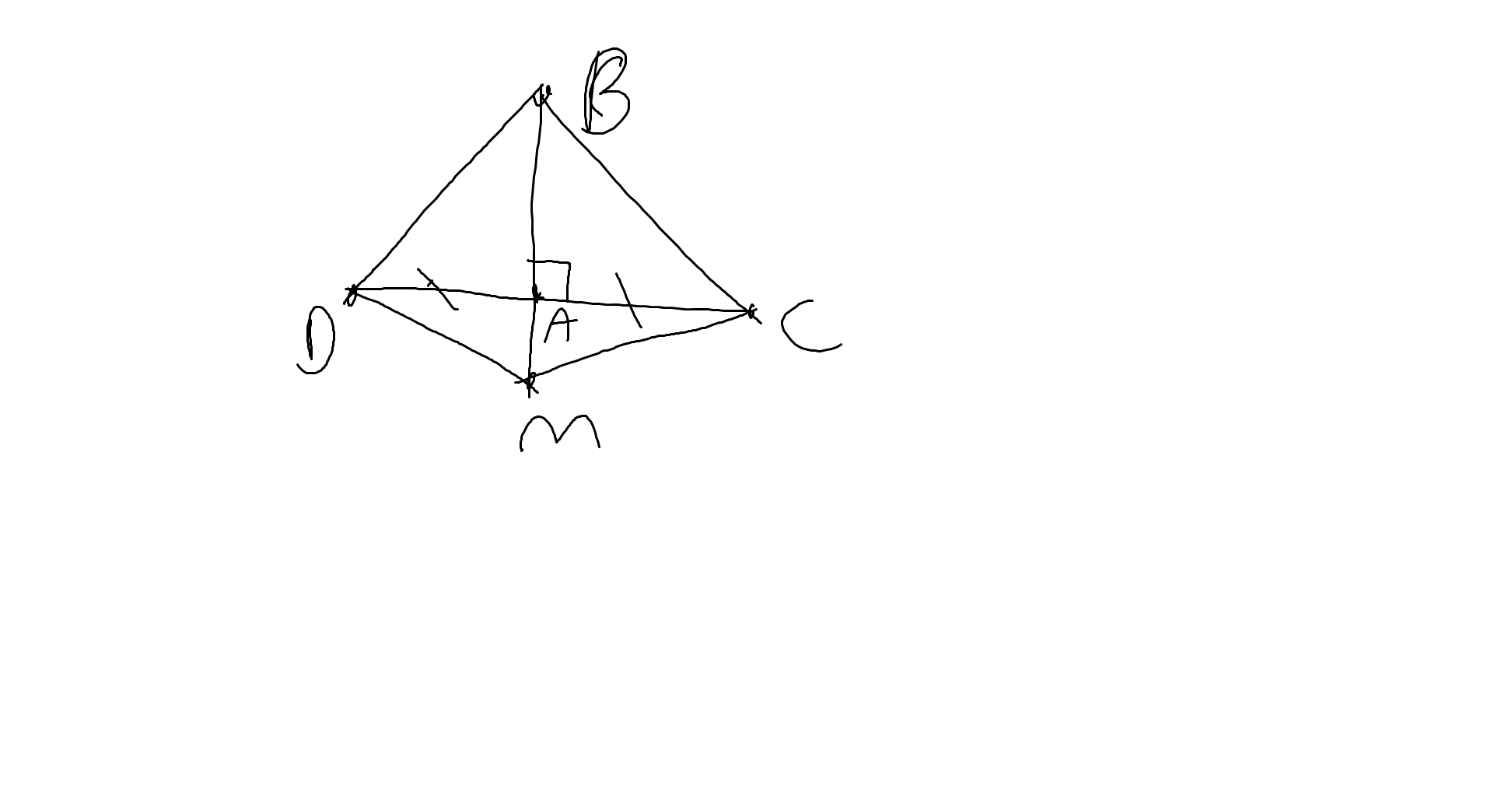
b: ΔABD=ΔABC

=>BD=BC

ΔABD=ΔABC

=>\(\widehat{ABD}=\widehat{ABC}\)

=>\(\widehat{MBC}=\widehat{MBD}\)

Xét ΔMBC và ΔMBD có

MB chung

\(\widehat{MBC}=\widehat{MBD}\)

BC=BD

Do đó: ΔMBC=ΔMBD

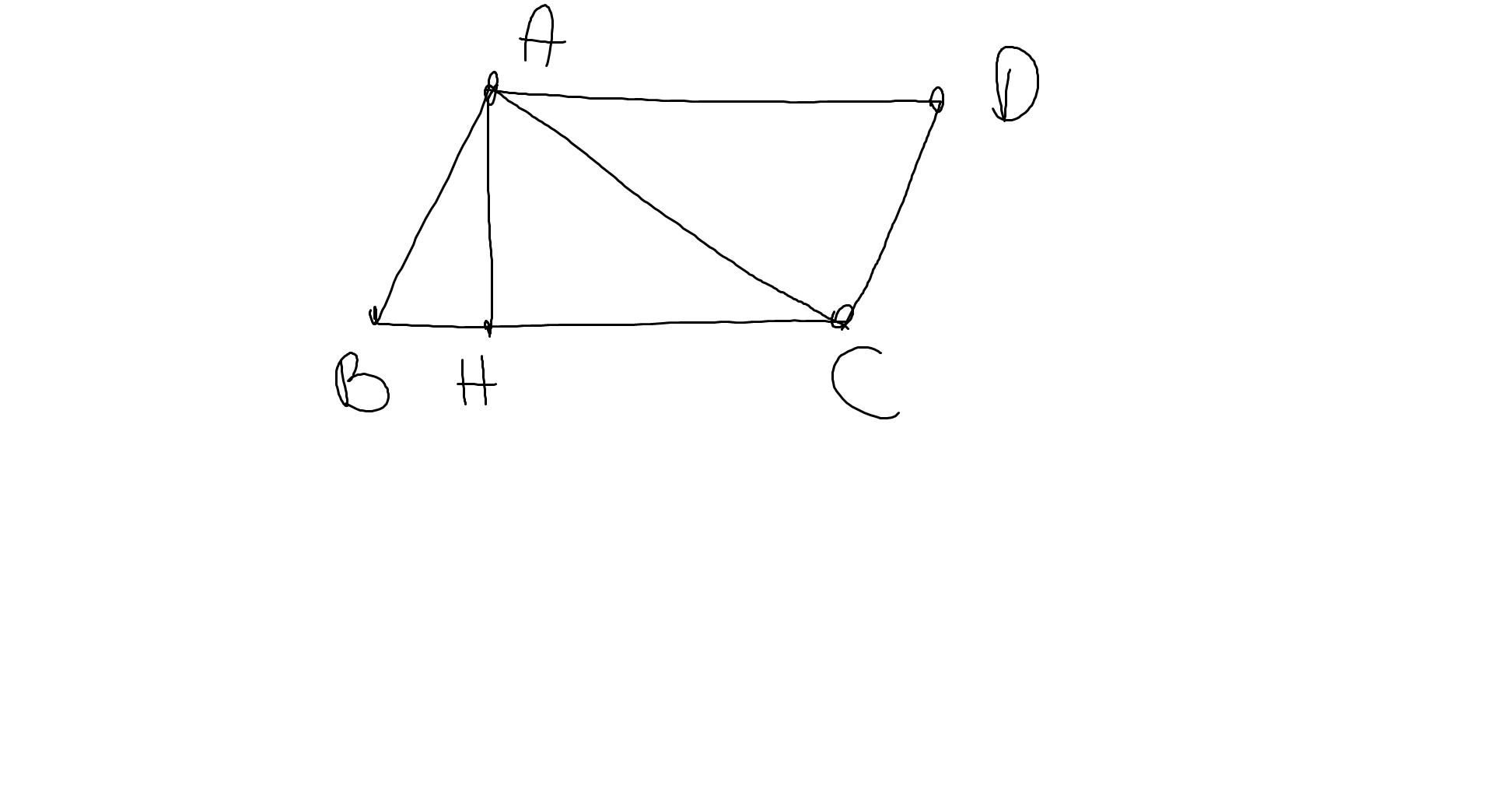
a: Xét ΔABC và ΔCDA có

AB=CD

AC chung

BC=DA

Do đó: ΔABC=ΔCDA

=>\(\widehat{BAC}=\widehat{DCA}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD

b: ΔABC=ΔCDA

=>\(\widehat{ACB}=\widehat{DAC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

mà AH\(\perp\)BC

nên AH\(\perp\)AD

a: Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMEB

=>\(\widehat{MAC}=\widehat{MEB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//EB

b: Xét ΔMAI và ΔMEK có

MA=ME

\(\widehat{MAI}=\widehat{MEK}\)(cmt)

AI=EK

Do đó: ΔMAI=ΔMEK

=>\(\widehat{AMI}=\widehat{EMK}\)

=>\(\widehat{EMK}+\widehat{EMI}=180^0\)

=>I,M,K thẳng hàng

27 : \(x\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)

27 : \(x\) =  \(\dfrac{6}{30}-\dfrac{5}{30}\)

 27 : \(x\) = \(\dfrac{1}{30}\)

  \(x\) = 27 : \(\dfrac{1}{30}\) 

   \(x\) = 810

Em cần làm gì với biể thức này? 

xy - 2x + y = 9  (x,y E N)

x(y - 2) + y-2+2 = 9

x(y-2)  + (y-2) = 9-2 = 7

(x+1)(y-2) = 7

Suy ra x+1 thuộc Ư(7) = {1;7)  (do x E N nên x+1 E N)

TH1 : x+1 = 1

Suy ra y-2 = 7

Suy ra x=0 ; y = 9

Th2:  x+1 = 7

Suy ra y-2 = 1

Suy ra x = 6 ; y = 3

Vậy ........

Gọi \(x\) (học sinh) là số học sinh cần tìm \(\left(x\in N;30\le x\le40\right)\)

Do khi xếp hàng 3; 6; 9 đều vừa đủ nên \(x⋮3;x⋮6;x⋮9\)

\(\Rightarrow x\in BC\left(3;6;9\right)\)

Ta có:

\(3=3\)

\(6=2.3\)

\(9=3^2\)

\(\Rightarrow BCNN\left(3;6;9\right)=2.3^2=18\)

\(\Rightarrow x\in\left\{0;18;36;54;...\right\}\)

Mà \(30\le x\le40\)

\(\Rightarrow x=36\)

Vậy lớp 6C có 36 học sinh

101

a) Sau a phút, lượng nước có trong bể là:

\(x-y\left(l\right)\)

b) Sau b phút, vòi nước chảy vào được số lít nước là: \(bx\left(l\right)\)

Lượng nước trong bể:

\(5+x-y+bx\left(l\right)\)