∆ABC có:

AB = BC (gt)

⇒ ∆ABC cân tại B

⇒ ∠BAC = ∠BCA (1)

Do AC là tia phân giác của ∠BAD (gt)

⇒ ∠DAC = ∠BAC (2)

Từ (1) và (2) ⇒ ∠BCA = ∠DAC

Mà ∠BCA và ∠DAC là hai góc so le trong

⇒ BC // AD

⇒ ABCD là hình thang

\(\dfrac{n^2-2n+5}{n+2}=\dfrac{n^2+2n-4n+5}{n+2}=n-\dfrac{4n-5}{n+2}\)

\(=n-\dfrac{4\left(n+2\right)-13}{n+2}=n-4-\dfrac{13}{n+2}\)

Do n - 4 nguyên => 13/n+2 nguyên 

\(n+2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)

Bạn xem lại dòng thứ ba, phải đối dấu thành: n - 4 + 13/(n+2) mới đúng nhé

Kho thứ nhất có số thóc là:

765 : (2 + 7) x 2 = 170 (tấn)

Tổng số thóc của kho thứ nhất và thứ 2 là:

765 - 170 = 595 (tấn)

Kho thứ nhất có số thóc là:

(595 - 95) : 2 = 250 (tấn)

Kho thứ 2 có số thóc là:

250 + 95 = 345 (tấn)

Đáp số: Kho thứ nhất: 250 tấn thóc

              Kho thứ hai: 345 tấn thóc

              Kho thứ ba: 170 tấn thóc

Kho thứ ba có số thóc là:

\(765:\left(2+7\right)\times2=170\) (tấn)

Tổng số thóc của kho thứ nhất và kho thứ hai là:

\(765-170=595\) (tấn)

Kho thứ nhất có số thóc là:

\(\left(595-95\right):2=250\) (tấn)

Kho thứ hai có số thóc là:

\(250+95=345\) (tấn)

Đáp số:...

Hàng nghìn có 4 cách chọn ( Là các số 5, 9, 4, 1)

Hàng trăm có 4 cách chọn (Vì khác nhau nên bỏ 1 số trong 4 số ở hàng nghìn nhưng nhận thêm 0 nên vẫn có 4 cách chọn)

Hàng chục có 3 cách chọn (Tương tự vì khác nhau nên số cách chọn giảm đi 1)

Hàng đơn vị có 2 cách chọn

Vậy lập được: 4x4x3x2=96 (số) thỏa mãn yêu cầu đề bài

Phần mở ngoặc mình giải thích thêm cho bạn dễ hiểu nhé.

Cho 4 chữ số có dạng \(\overline{abcd}\)

Với a khác 0 

a có 4 cách chọn 

b có 4 cách chọn 

c có 3 cách chọn 

d có 2 cách chọn 

=> 96 cách chọn 

45 kg 5 dag = 45050 g

456 yến = 45,6 tạ

345 dam² = 3,45 hm²

Chi hái được số quả táo là:

20 x 2 = 40 ( quả )

Nhung hái được số quả táo là:

( 20 + 40 ) : 2 = 30 ( quả )

Cả 3 bạn hái được số quả táo là:

20 + 40 + 30 = 90 ( quả )

Đ/s : 90 quả táo

cả 3 bạn hái được 80 quả

`#3107.101107`

\(\dfrac{8}{5}-\dfrac{1}{5}\div\left(x+\dfrac{2}{7}\right)=1\\ \Rightarrow\dfrac{1}{5}\div\left(x+\dfrac{2}{7}\right)=\dfrac{8}{5}-1\\ \Rightarrow\dfrac{1}{5}\div\left(x+\dfrac{2}{7}\right)=\dfrac{3}{5}\\ \Rightarrow x+\dfrac{2}{7}=\dfrac{1}{5}\div\dfrac{3}{5}\\ \Rightarrow x+\dfrac{2}{7}=\dfrac{1}{3}\\ \Rightarrow x=\dfrac{1}{3}-\dfrac{2}{7}\\ \Rightarrow x=\dfrac{1}{21}\)

Vậy, \(x=\dfrac{1}{21}.\)

`#3107.101107`

`1.`

Số hạng của tổng B:

`(99 - 1) \div 1 + 1 = 99` (số hạng)

Giá trị của tổng B:

`(99 + 1) \cdot 99 \div 2 = 4950`

$55+88=53+90=143$

55 + 88 = 143

143 = ... + 90 

 ...   = 143 - 90

... = 53

Vậy 55 + 88 = 53 + 90 = 143 

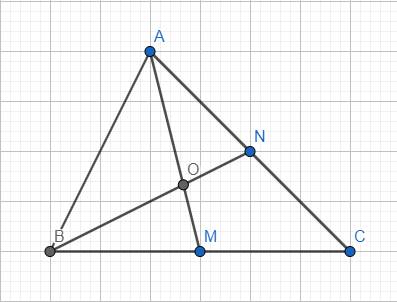
\(\text{△ABC}\) có: \(AM,BN\) là 2 đường trung tuyến (gt)

Mà \(O\) là giao điểm của \(AM\) và \(BN\) nên:

\(O\) là trọng tâm của \(\text{△ABC}\)

\(\Rightarrow ON=\dfrac{1}{2}OB\) (theo tính chất ba đường trung tuyến trong tam giác)

Thay \(ON=1\) được:

\(OB=2\cdot ON=2\cdot1=2\)

Vậy \(OB=2\)

Vì ON = 1 , và O là trọng tâm, thì OB sẽ là 2 lần ON , tức là:

OB = 2 x ON = 2 x 1 = 2

Vậy độ dài của OB là 2.