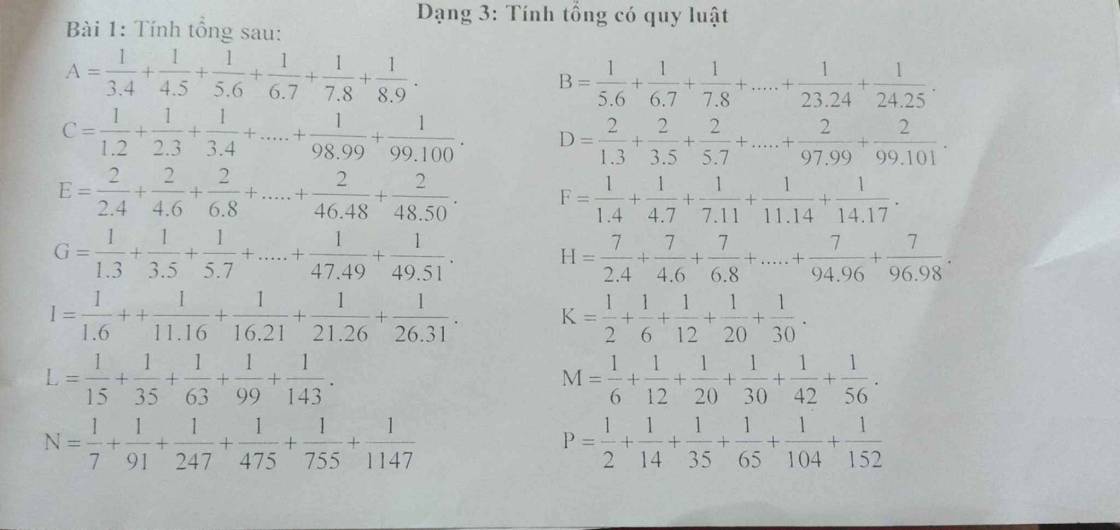
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lúc đầu thùng nhỏ có số lít nước mắm là:
8,7 + 4,29 = 12,99 (l)
Lúc đầu thùng to có số lít nước mắm là:
12,99 + 3,6 = 16,59 (l)
Đs....
tìm giá trị lớn nhất của P = \(\dfrac{|x-2022|-|x-2023|+|x-2024|+2022}{|x-2022|+|x-2023|+|x-2024|}\)


Cảm ơn em đã lựa chọn olm là môi trường học tập và giao lưu với cộng đồng tri thức trong và ngoài nước mà em yêu thương và tin tưởng. Cảm ơn những trải nghiệm và đánh giá của em trong quá trình học tập trên olm.
olm chúc em học tập vui vẻ và hiệu quả cùng olm em nhá!

\(k^2=\left(m+1\right)\left(m^2+2m\right)\) là số chính phương
\(\Rightarrow k^2=m\left(m+1\right)\left(m+2\right)\ge0\)
Lập bảng xét dấu
| \(m\) | \(-2\) \(-1\) \(0\) |
| \(m\) | \(-\) \(|\) \(-\) \(|\) \(-\) \(0\) \(+\) |
| \(m+1\) | \(-\) \(|\) \(-\) \(0\) \(+\) \(|\) \(+\) |
| \(m+2\) | \(-\) \(0\) \(+\) \(|\) \(+\) \(|\) \(+\) |
| \(m\left(m+1\right)\left(m+2\right)\) | \(-\) \(0\) \(+\) \(0\) \(-\) \(0\) \(+\) |
\(\Rightarrow\left[{}\begin{matrix}-2\le m\le0\\m>0\end{matrix}\right.\)
\(TH1:\) \(-2\le m\le0\Rightarrow m\in\left\{-2;-1;0\right\}\) thỏa mãn \(k^2=0\ge0\)
\(TH2:\) \(m>0\)
\(k^2=\left(m+1\right)\left(m^2+2m\right)\)
\(d=UC\left(m+1;m^2+2m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}m+1⋮d\\m^2+2m⋮d\end{matrix}\right.\)
\(\Rightarrow m^2+2m-2\left(m+1\right)⋮d\)
\(\Rightarrow m^2+2m-2m-1⋮d\)
\(\Rightarrow-1⋮d\)
\(\Rightarrow d\in\left\{-1;1\right\}\)
\(\Rightarrow\left(m+1\right)\left(m^2+2m\right)\) là số chính phương khi chúng là số chính phương.
Ta lại có :
\(\left(m+1\right)\left(m^2+2m\right)=m\left(m+1\right)\left(m+2\right)\) là tích của 3 số liên tiếp nhau không phải là số chính phương khi m>0
Vậy \(m\in\left\{-2;-1;0\right\}\) thỏa mãn đề bài

Lời giải:
Xét tỉ số:
\(\frac{100!}{2^{300}}=\frac{100!}{8^{100}}=\frac{1}{8}.\frac{2}{8}.\frac{3}{8}.....\frac{99}{8}.\frac{100}{8}\)
\(=(\frac{1}{8}.\frac{64}{8})(\frac{2}{8}.\frac{32}{8})(\frac{3}{8}.\frac{22}{8})(\frac{4}{8}.\frac{16}{8})(\frac{5}{8}.\frac{13}{8})(\frac{6}{8}.\frac{11}{8})(\frac{7}{8}.\frac{10}{8}).\frac{8}{8}.\frac{9}{8}.\frac{12}{8}.\frac{14}{8}.\frac{15}{8}.\frac{17}{8}....\frac{31}{8}.\frac{33}{8}...\frac{65}{8}...\frac{100}{8}\)
\(>1.1....1=1\)
$\Rightarrow 100!> 2^{300}$

Chuồng thứ 2 đẻ số quả trứng là:
\(535\times2=1070\left(quả.trứng\right)\)
Cả 2 chuồng có số quả trứng là:
\(535+1070=1605\left(quả.trứng\right)\)
Chuồng thứ 2 gà đẻ số quả trứng là:
535.2=1070(quả)
Cả hai chuồng gà đẻ được số quả trứng là:
535+1070=1605(quả)
Vậy cả 2 chuồng gà đẻ được 1605 quả trứng

Nhà Nam còn số con gà là:
\(1520-532=988\left(con.gà\right)\)
Vậy nhà Nam có \(988\) con gà.

A = \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{6.7}\)+ \(\dfrac{1}{7.8}\)+ \(\dfrac{1}{8.9}\)
A = \(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{8}\)+\(\dfrac{1}{8}\)-\(\dfrac{1}{9}\)
A = \(\dfrac{1}{3}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{2}{9}\)
B = \(\dfrac{1}{5.6}\)+ \(\dfrac{1}{6.7}\)+\(\dfrac{1}{7.8}\)+...+\(\dfrac{1}{23.24}\)+\(\dfrac{1}{24.25}\)
B = \(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{8}\)+...+\(\dfrac{1}{23}\)-\(\dfrac{1}{24}\)+ \(\dfrac{1}{24}\)-\(\dfrac{1}{25}\)
B = \(\dfrac{1}{5}\) - \(\dfrac{1}{25}\)
B = \(\dfrac{4}{25}\)