6777

Lớp 1 ? 

X x 123 = 322 + 776

X x 123 = 1098

X = 1098 : 123

X = 1098/123

Chú ý lần sau không ghi nội dung không liên quan đến bài tập bạn nhé

\(X\times123=322+766\\ \text{X}\times123=1088\\ \text{X}=1=1088\div123\\ \text{X}=\dfrac{1088}{123}\)

a: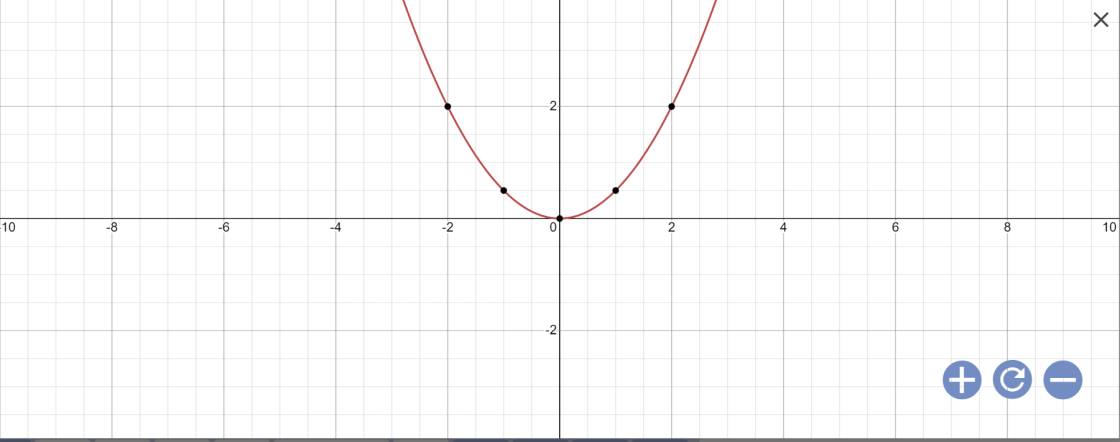 

b: Thay x=0 và y=-2 vào (d1), ta được:

\(a\cdot0+b=-2\)

=>b=-2

=>(d1): y=ax-2

Thay x=1 và y=3 vào (d1), ta được:

\(a\cdot1-2=3\)

=>a-2=3

=>a=5

Vậy: (d1): y=5x-2

c: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=2x+m\)

=>\(x^2=4x+2m\)

=>\(x^2-4x-2m=0\)

\(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(-2m\right)=8m+16\)

Để (P) cắt (d2) tại hai điểm phân biệt thì 8m+16>0

=>8m>-16

=>m>-2

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-2m\end{matrix}\right.\)

\(x_1+x_2-2x_1x_2=2024\)

=>\(4-2\cdot\left(-2m\right)=2024\)

=>4m+4=2024

=>m+1=506

=>m=505(nhận)

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\)

\(\Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]-105=0\)

\(\Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)-105=0\) (1)

Đặt \(x^2+10x+20=t\), khi đó (1) trở thành:

\(\left(t-4\right)\left(t+4\right)-105=0\)

\(\Leftrightarrow t^2-16-105=0\)

\(\Leftrightarrow t^2-11^2=0\)

\(\Leftrightarrow\left(t-11\right)\left(t+11\right)=0\)

\(\Rightarrow\left(x^2+10x+20-11\right)\left(x^2+10x+20+11\right)=0\)

\(\Leftrightarrow\left(x^2+10x+9\right)\left(x^2+10x+31\right)=0\)

\(\Leftrightarrow\left(x^2+9x+x+9\right)\left[\left(x+5\right)^2+6\right]=0\)

\(\Leftrightarrow x\left(x+9\right)+\left(x+9\right)=0\) (vì \(\left(x+5\right)^2+6>0;\forall x\))

\(\Leftrightarrow\left(x+9\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+9=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=-1\end{matrix}\right.\)

Vậy phương trình đã cho có tập nghiệm là $S=\{-9;-1\}$.

$Toru$

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\\ \Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]=105\\ \Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)=105\\ \Leftrightarrow\left(x^2+10x+20-4\right)\left(x^2+10x+20+4\right)=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2-4^2=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2=121\\ \)

\(\Rightarrow\left[{}\begin{matrix}x^2+10x+20=11\left(1\right)\\x^2+10x+20=-11\left(2\right)\end{matrix}\right.\)

Giải (1):

\(x^2+10x+9=0\\ \Leftrightarrow\left(x^2+x\right)+\left(9x+9\right)=0\\ \Leftrightarrow x\left(x+1\right)+9\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-9\end{matrix}\right.\)

Giải (2):

Nhận thấy: \(x^2+10x+20=\left(x+5\right)^2-5\ge-5\forall x\inℝ\)

Vậy pt (2) vô nghiệm

Vậy tập nghiệm pt là: \(S=\left\{-1;-9\right\}\)

Mình nghĩ là bằng nhau.

`060° = 60°`nhé

\(x+\sqrt{x+2}=0\left(ĐK:x\ge-2\right)\)

\(\Leftrightarrow x+1+\left(\sqrt{x+2}-1\right)=0\\ \Leftrightarrow x+1+\dfrac{x+2-1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow x+1+\dfrac{x+1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow\left(x+1\right)\left(1+\dfrac{1}{\sqrt{x+2}+1}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\end{matrix}\right.\Leftrightarrow x=-1\left(TMDK\right)\)

Vậy pt có nghiệm duy nhất: x=-1

Mình giải thích thêm phần này nhé:

\(1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\)

Vì với mọi x thuộc ĐK:

\(\sqrt{x+2}\ge0\Rightarrow\sqrt{x+2}+1>0\\ \Rightarrow\dfrac{1}{\sqrt{x+2}+1}>0\\ \Rightarrow VT=1+\dfrac{1}{\sqrt{x+2}+1}>0=VP\)

Do VT > VP nên không thể xảy ra dấu = 

Dẫn đến ptvn bạn nhé

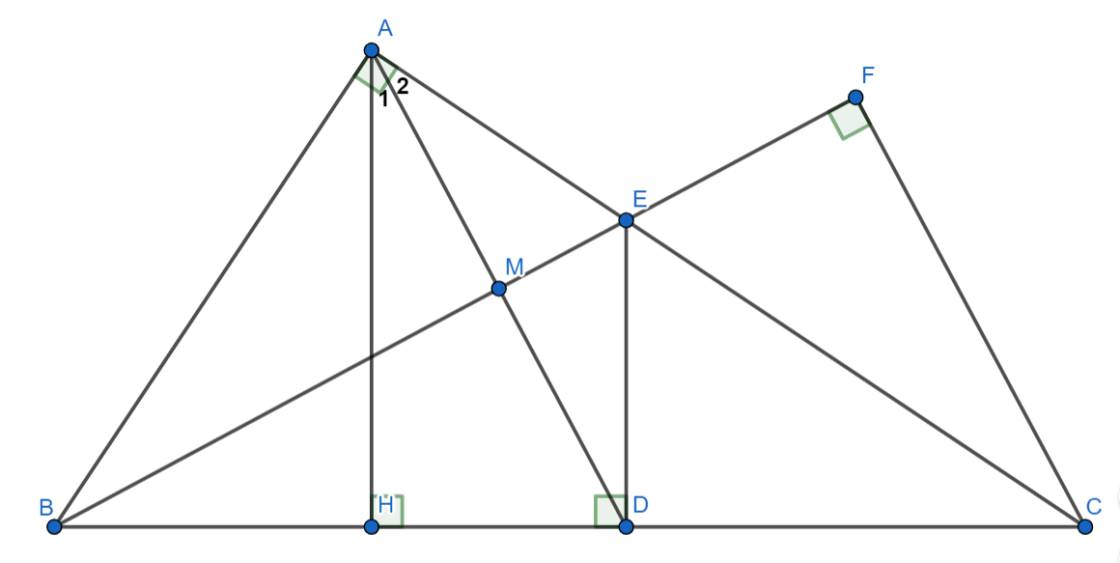
a) Xét \(\Delta BAE\) và \(\Delta BDE\) có:  

\(\left\{{}\begin{matrix}\widehat{BAE}=\widehat{BDE}=90^{\circ}\left(\Delta ABC\text{ vuông tại }A;DE\perp BC\right)\\BE\text{ chung}\\BA=BD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta BAE=\Delta BDE\left(ch-cgv\right)\) (đpcm)

b) Ta có: \(BD=BA\Rightarrow B\) là điểm nằm trên đường trung trực của AD (1)

Vì \(\Delta BAE=\Delta BDE\left(cmt\right)\Rightarrow AE=DE\) (2 cạnh tương ứng)

\(\Rightarrow E\) là điểm nằm trên đường trung trực của AD (2)

Từ (1) và (2) \(\Rightarrow BE\) là đường trung trực của AD

Mà: \(BE\cap AD=\left\{M\right\}\) nên \(BM\perp AD\)

hay \(BM\) là đường cao của \(\Delta ABD\) (đpcm)

c) Vì \(AE=DE\Rightarrow\Delta ADE\) cân tại E (t/c)

\(\Rightarrow\widehat{A_2}=\widehat{EDA}\) (t/c) (3)

Lại có: \(\begin{cases} AH\perp CD\\ DE\perp CD \end{cases} \Rightarrow AH//DE\)

\(\Rightarrow\widehat{A_1}=\widehat{EDA}\) (2 góc so le trong) (4)

Từ (3) và (4) \(\Rightarrow\widehat{A_1}=\widehat{A_2}\)

Mà tia AD nằm trong \(\widehat{HAC}\)

nên tia AD là tia phân giác của \(\widehat{HAC}\) (đpcm)

d) Xét \(\Delta EBC\) có: \(\left\{{}\begin{matrix}AB\perp EC\left(\Delta ABC\text{ vuông tại }A;E\in AC\right)\\DE\perp BC\left(gt\right)\\CF\perp BE\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AB,DE,CF\) đồng quy (t/c) (đpcm)

$\text{#}Toru$

$Toru$

Lời giải:

$BCNN(m,n) = 2^4.3^5.5.7^6.11^4$

$ BCNN (m,n) = 2^4.3^5.5.7^6.11^4$

Lời giải:

$BCNN(m,n) = 2^4.3^5.5.7^6.11^4$

câu a

\(x\cdot\dfrac{1}{2}+2\cdot\dfrac{2}{3}=2\cdot\dfrac{3}{4}\\ \dfrac{1}{2}x+\dfrac{4}{3}=\dfrac{3}{2}\\ \dfrac{1}{2}x=\dfrac{1}{6}\\ x=\dfrac{1}{3}\)

câu b

\(2\cdot\dfrac{1}{2}+x:1\cdot\dfrac{1}{3}=\dfrac{3}{4}\\ 1+x:1\cdot\dfrac{1}{3}=\dfrac{3}{4}\\ x:1\cdot\dfrac{1}{3}=\dfrac{-1}{4}\\ x:1=-\dfrac{3}{4}\\ x=\dfrac{-3}{4}\)

Bạn ấn vào biểu tượng Σ ở góc bên trái để nhập công thức toán học nhé!