Bài 1: Viết các biểu thức sau thành tích
a,27+8y^3
b,1/8x^3-1
c,x^3+27
Giúp mình với nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-18x+81=0\)
\(\Leftrightarrow x^2-2.9x+9^2=0\)
\(\Leftrightarrow\left(x-9\right)^2=0\Leftrightarrow x=9\)

a. Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có:
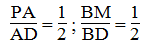
Suy ra:
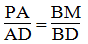
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong ΔACD, ta có
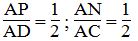
Suy ra:
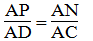
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
b. Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2

3(x + 1)2 - 3x(x + 2) = 1
<=> 3x2 + 6x + 3 - 3x2 - 6x = 1
<=> 3 = 1 (vô lí)
Vậy phương trình vô nghiệm.
(x - 1)3 - (x + 3)(x2 - 3x + 9) + 3(x2 - 4) = 2
<=> x3 - 3x2 + 3x - 1 - x3 - 27 + 3x2 - 12 = 2
<=> 3x - 40 = 2
<=> 3x = 42
<=> x = 14
Vậy S = { 14 }.
(x + 2)(x2 - 2x + 4) - x(x2 + 2) = 15
<=> x3 + 8 - x3 - 2x = 15
<=> - 2x + 8 = 15
<=> - 2x = 7
<=> x = - 7/2
Vậy S = { - 7/2 }.

M = x^2 - 4x
= x^2 - 4x + 4 - 4
= (x^2 - 4x + 4 ) - 4
=(x - 2 )^2 - 4
Vì (x - 2 )^2 \(\ge\)0 => (x - 2 )^2 - 4 \(\ge\) - 4 ( với \(\forall\) x )
Dấu '' = '' sảy ra <=> (x - 2 )^2 = 0
<=> x - 2 = 0
<=> x = 2
Vậy min M = - 4 Khi x = 2
M = x2 - 4x = (x2 - 4x + 4) - 4 = (x - 2)2 - 4
Vì (x - 2)2 ≥ 0 với mọi x
Mà (x - 2)2 - 4 ≥ - 4 với mọi x
Vậy M đạt giá trị nhỏ nhất <=> (x - 2)2 = 0 <=> x = 2
D = x2 - 2x + 5 = (x2 - 2x + 1) + 4 = (x - 1)2 + 4
Vì (x - 1)2 ≥ 0 với mọi x
Mà (x - 1)2 + 4 ≥ 4 với mọi x
=> (x - 1)2 + 4 > 0 (luôn dương với mọi x)
=> x2 - 2x + 5 > 0 (luôn dương với mọi x)

x^3- 4x^2-8x+8
= (x+2)(x^2-6x+4)
nha bạn chúc bạn học tốt nha

x^3+x^2-2x-8
= (x-2)(x^2+3x+4)
nah bạn chúc bạn học tốt nha
x3 + x2 - 2x - 8
= ( x3 - 8 ) + ( x2 - 2x )
= ( x - 2 ) . ( x2 + 2x + 4 ) + x ( x - 2 )
= ( x - 2 ) .( x2 + 2x + 4 + x )
= ( x-2 ) . ( x2 + 3x + 4 )

2x^2-xy+5y-25
= -(xy-5y-2x^2+25)
nah bạn chúc bạn học tốt nha
a,33+(2y)^3
=(2y+3)(4y2+6y+9)
b,tương tự câu a)
c,tương tự câu a)
Trả lời:
\(a,27+8y^3=\left(3+2y\right)\left(9-6y+4y^2\right)\)
\(b,\frac{1}{8}x^3-1=\left(\frac{1}{2}x-1\right)\left(\frac{1}{4}x^2+\frac{1}{2}x+1\right)\)
\(c,x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)