28 D

29 B

30 D

31 A

32 C

33 C

34 A

35 What were you doing at 9 o'clock yesterday?

36 There are many speciality shops in a shopping center

37 Shopping centers offer a wide range of products

38 When I was going shopping with my mother yesterday, I saw a thief

39 My mother usually goes to the grocery store

40 When she was working in the field, the tornado came

I saw an alien walking when I was walking

I saw an alien when I was walking

3. Chứng minh công thức:

AF/AB + BE/BC + CN/CA = 1 trong tam giác ABC

Giả thiết:

• Tam giác ABC.
• Các điểm F, E, N lần lượt nằm trên các cạnh AB, BC, CA.

Cách chứng minh:

Trường hợp đặc biệt:
Nếu F, E, N là các điểm chia các cạnh theo cùng một tỉ lệ (ví dụ: F chia AB theo tỉ lệ x, E chia BC theo tỉ lệ y, N chia CA theo tỉ lệ z sao cho x + y + z = 1).

Chứng minh tổng quát:

• Gọi AF = x·AB, BE = y·BC, CN = z·CA, với x, y, z ∈ (0;1).
• Khi đó:
  \(\frac{A F}{A B} + \frac{B E}{B C} + \frac{C N}{C A} = x + y + z\)
• Nếu ba điểm F, E, N chia ba cạnh theo tỉ lệ x, y, z sao cho x + y + z = 1, thì tổng trên bằng 1.

Trường hợp đặc biệt:
Nếu F, E, N là trung điểm các cạnh, thì mỗi phân số đều bằng 1/2, tổng lại là 3/2 ≠ 1.
Vậy công thức đúng khi ba điểm chia ba cạnh theo tỉ lệ x, y, z với x + y + z = 1.

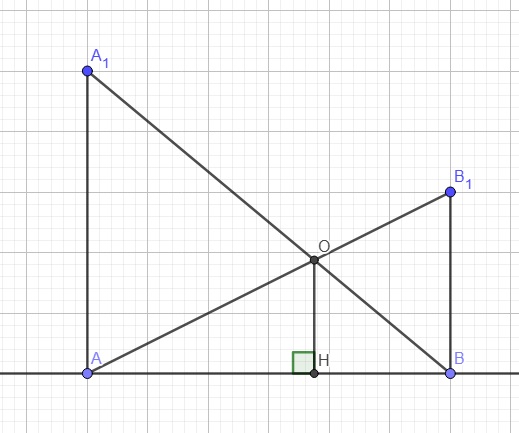
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d

Giải chi tiết:

Bước 1: Xác định phương trình đường thẳng CD
Giả sử:

• Tọa độ của điểm A và B thay đổi, nhưng luôn thỏa mãn điều kiện bài toán.
• Điểm C và D được xác định dựa trên A và B qua một quy tắc cụ thể (ví dụ: trung điểm, hình chiếu, giao điểm đường phân giác...).
• Gọi phương trình đường thẳng CD có dạng:
  \(a x + b y + c = 0 (\text{ph}ụ\&\text{nbsp};\text{thu}ộ\text{c}\&\text{nbsp};\text{v} \overset{ˋ}{\text{a}} \text{o}\&\text{nbsp};\text{t}ọ\text{a}\&\text{nbsp};độ\&\text{nbsp};\text{A},\&\text{nbsp};\text{B})\)

Bước 2: Tìm điểm cố định mà CD luôn đi qua

• Giả định tồn tại điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\) sao cho CD luôn đi qua \(M\) với mọi vị trí của A và B (\(A \neq B\)).
• Thay \(M \left(\right. x_{0} , y_{0} \left.\right)\) vào phương trình CD:
  \(a \left(\right. x_{0} , y_{0} , A , B \left.\right) \cdot x_{0} + b \left(\right. x_{0} , y_{0} , A , B \left.\right) \cdot y_{0} + c \left(\right. x_{0} , y_{0} , A , B \left.\right) = 0 \forall A , B\)
• Phân tích phương trình:
  Biến đổi phương trình về dạng đa thức theo tham số liên quan đến A và B. Để phương trình đúng với mọi A, B, hệ số của các hạng tử chứa tham số phải bằng 0.

Bước 3: Giải hệ phương trình

• Ví dụ: Nếu phương trình có dạng:
  \(\left(\right. m + 1 \left.\right) x_{0} - \left(\right. 2 m - 3 \left.\right) y_{0} + 5 = 0 \forall m\)
• • Tách hệ số của \(m\):
    \(m \left(\right. x_{0} - 2 y_{0} \left.\right) + \left(\right. x_{0} + 3 y_{0} + 5 \left.\right) = 0 \forall m\)
  • Đồng nhất hệ số:
    \(\left{\right. x_{0} - 2 y_{0} = 0 \\ x_{0} + 3 y_{0} + 5 = 0\)
  • Giải hệ:
    \(x_{0} = 2 y_{0} 2 y_{0} + 3 y_{0} + 5 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y_{0} = - 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x_{0} = - 2\)
  • Kết luận: Điểm cố định là \(M \left(\right. - 2 , - 1 \left.\right)\).

Bước 4: Kiểm tra lại

• Thay \(M \left(\right. x_{0} , y_{0} \left.\right)\) vào phương trình CD với các vị trí khác nhau của A, B để xác nhận tính đúng đắn.

Ví dụ minh họa:
Cho tam giác ABC cố định. Trên AB lấy điểm D di động, trên AC lấy điểm E di động sao cho \(A D = C E\). Chứng minh DE luôn đi qua một điểm cố định.

Giải:

• Bước 1: Chọn hệ trục tọa độ, giả sử \(A \left(\right. 0 , 0 \left.\right)\), \(B \left(\right. 1 , 0 \left.\right)\), \(C \left(\right. 0 , 1 \left.\right)\).
• Bước 2: Gọi \(D \left(\right. t , 0 \left.\right)\) trên AB và \(E \left(\right. 0 , t \left.\right)\) trên AC (vì \(A D = C E = t\)).
• Bước 3: Phương trình DE:
  \(\frac{x - t}{- t} = \frac{y}{t - 0} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x + y = t\)
• Bước 4: Phương trình \(x + y = t\) phụ thuộc vào \(t\). Để DE đi qua điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\):
  \(x_{0} + y_{0} = t \forall t \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x_{0} + y_{0} = 0\)
  Chọn \(M \left(\right. 1 , - 1 \left.\right)\) (nằm trên đường thẳng \(x + y = 0\)).

Kết luận: DE luôn đi qua điểm cố định \(M \left(\right. 1 , - 1 \left.\right)\).

Đáp án:
Đường thẳng CD luôn đi qua điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\) được xác định bằng cách giải hệ phương trình từ phương trình tổng quát của CD145.

Giải chi tiết:

Bước 1: Xác định vị trí các điểm P, I, K, Q
Giả thiết:

• P là trung điểm của AB.
• Q là trung điểm của AC.
• I và K lần lượt là trung điểm của BC và CA.

Bước 2: Tính chất hình học

• Đường trung bình PQ của tam giác ABC song song với BC và có độ dài bằng \(\frac{1}{2} B C\).
• Tứ giác PIKQ là hình bình hành (do PQ // IK và PI // QK).

Bước 3: Tính diện tích PIKQ

• Diện tích hình bình hành PIKQ = \(\frac{1}{2} \times \text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{ABC}\).
• Giả sử tam giác ABC có diện tích \(S_{A B C}\), khi đó:
  \(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Ví dụ minh họa:
Cho tam giác ABC có diện tích \(20 \textrm{ } \text{cm}^{2}\).

• Diện tích tứ giác PIKQ là:
  \(S_{P I K Q} = \frac{1}{2} \times 20 = 10 \textrm{ } \text{cm}^{2}\)

Kết luận:
Diện tích tứ giác PIKQ bằng một nửa diện tích tam giác ABC nếu các điểm P, I, K, Q là trung điểm của các cạnh134.

Công thức tổng quát:

\(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Đáp án:
Diện tích tứ giác PIKQ là \(\boxed{\frac{1}{2} S_{A B C}}\).

Giải chi tiết:

Bước 1: Xác định vị trí các điểm P, I, K, Q
Giả thiết:

• P là trung điểm của AB.
• Q là trung điểm của AC.
• I và K lần lượt là trung điểm của BC và CA.

Bước 2: Tính chất hình học

• Đường trung bình PQ của tam giác ABC song song với BC và có độ dài bằng \(\frac{1}{2} B C\).
• Tứ giác PIKQ là hình bình hành (do PQ // IK và PI // QK).

Bước 3: Tính diện tích PIKQ

• Diện tích hình bình hành PIKQ = \(\frac{1}{2} \times \text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{ABC}\).
• Giả sử tam giác ABC có diện tích \(S_{A B C}\), khi đó:
  \(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Ví dụ minh họa:
Cho tam giác ABC có diện tích \(20 \textrm{ } \text{cm}^{2}\).

• Diện tích tứ giác PIKQ là:
  \(S_{P I K Q} = \frac{1}{2} \times 20 = 10 \textrm{ } \text{cm}^{2}\)

Kết luận:
Diện tích tứ giác PIKQ bằng một nửa diện tích tam giác ABC nếu các điểm P, I, K, Q là trung điểm của các cạnh134.

Công thức tổng quát:

\(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Đáp án:
Diện tích tứ giác PIKQ là \(\boxed{\frac{1}{2} S_{A B C}}\).

\(a=\frac72\) ​,b=3

f(2)=0

=>\(2^2+a\cdot2+b=0\)

=>2a+b=-4

=>b=-4-2a

=>\(f\left(x\right)=x^2+ax-2a-4\)

f(x) chia hết cho 2x-3

=>\(x^2+ax-2a-4⋮2x-3\)

=>\(x^2-1,5x+\left(a+1,5\right)x-\left(1,5a+2,25\right)+1,5a+2,25-2a-4⋮2x-3\)

=>-0,5a-1,75=0

=>0,5a=-1,75

=>a=-3,5

b=-4-2a=-4+7=3

nghĩa hàm ẩn: đừng sợ độ cao

hãy đối mặt vs nó

g khổ thơ sau:

Đề bài:
"Không có gì từ đến đâu còn quá muộn
Ngọt phải tháng ngày tích nhựa hoa
Sẽ thơm khi qua nắng lửa mùa bội thu
Trái một nắng hạ..."

Trả lời:
Các biện pháp tu từ trong khổ thơ trên gồm:

• Ẩn dụ:
• • "Ngọt phải tháng ngày tích nhựa hoa" (ẩn dụ cho thành quả phải trải qua quá trình tích lũy, rèn luyện).
  • "Sẽ thơm khi qua nắng lửa mùa bội thu" (ẩn dụ cho sự thành công, hạnh phúc sau khi vượt qua thử thách).
• Nhân hóa:
• • "Trái một nắng hạ" (trái được nhân hóa, như mang cảm xúc, trải nghiệm).
• Điệp ngữ:
• • "Không có gì từ đến đâu còn quá muộn" nhấn mạnh ý không bao giờ là quá muộn để bắt đầu hoặc thay đổi.