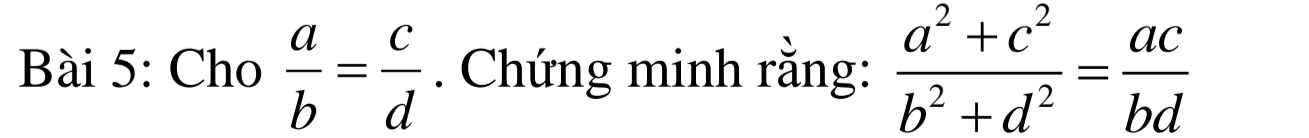 giải giúp mình với ai giải đc mình tick cho
giải giúp mình với ai giải đc mình tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{100}\\ =\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}+\dfrac{1}{100}\\ =\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{100}\\ =\dfrac{1}{4}-\dfrac{1}{10}+\dfrac{1}{100}\\ =\dfrac{25}{100}-\dfrac{10}{100}+\dfrac{1}{100}\\ =\dfrac{16}{100} =\dfrac{4}{25}\)
\(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{100}\\ =\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}+\dfrac{1}{100}\\ =\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{100}\\ =\dfrac{1}{4}-\dfrac{1}{10}+\dfrac{1}{100}\\ =\dfrac{4}{25}\)

\(a.\dfrac{2}{3}-\left(-\dfrac{1}{2}-x\right)=-\dfrac{4}{5}\\ \dfrac{2}{3}+\dfrac{1}{2}+x=-\dfrac{4}{5}\\ x=-\dfrac{4}{5}-\dfrac{2}{3}-\dfrac{1}{2}\\ x=-\dfrac{59}{30}\\ b.\left(-x-3\dfrac{1}{4}\right)-\left(1\dfrac{2}{3}-2\dfrac{3}{4}\right)=\dfrac{-5}{6}\\ \left(-x-\dfrac{13}{4}\right)-\left(\dfrac{5}{3}-\dfrac{11}{4}\right)=\dfrac{-5}{6}\\ -x-\dfrac{13}{4}-\dfrac{5}{3}+\dfrac{11}{4}=-\dfrac{5}{6}\\ -x-\dfrac{5}{3}-\dfrac{1}{2}=-\dfrac{5}{6}\\ x=\dfrac{5}{6}-\dfrac{5}{3}-\dfrac{1}{2}\\ x=-\dfrac{4}{3}\\ c.\dfrac{8}{23}\cdot\dfrac{46}{24}-\dfrac{1}{2}x=\dfrac{1}{3}\\ \dfrac{2}{3}-\dfrac{1}{2}x=\dfrac{1}{3}\\ \dfrac{1}{2}x=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}\\ x=\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{2}{3}\\ d.\dfrac{x-1}{16}=\dfrac{3}{x+1}\\ \left(x-1\right)\left(x+1\right)=3\cdot16=48\\ x^2-1=48\\ x^2=49\\ x^2=7^2\\ x=\pm7\)
\(e.\left(1,2\right)^3x^2=\left(1,2\right)^5\\ x^2=\dfrac{\left(1,2\right)^5}{\left(1,2\right)^3}\\ x^2=\left(1,2\right)^2\\ x=\pm1,2\\ f.\left(\dfrac{2}{3}x-\dfrac{1}{4}\right)^2=4\\ \left(\dfrac{2}{3}x-\dfrac{1}{4}\right)^2=2^2\\TH1:\dfrac{2}{3}x-\dfrac{1}{4}=2\\ \dfrac{2}{3}x=2+\dfrac{1}{4}=\dfrac{9}{4}\\ x=\dfrac{9}{4}:\dfrac{2}{3}=\dfrac{27}{8}\\ TH2:\dfrac{2}{3}x-\dfrac{1}{4}=-2\\ \dfrac{2}{3}x=-2+\dfrac{1}{4}=-\dfrac{7}{4}\\ x=\dfrac{-7}{4}:\dfrac{2}{3}=-\dfrac{21}{8}\\ g.\left(\dfrac{1}{6}x-3\right)^2=\dfrac{4}{9}\\ \left(\dfrac{1}{6}x-3\right)^2=\left(\dfrac{2}{3}\right)^2\\ TH1:\dfrac{1}{6}x-3=\dfrac{2}{3}\\ \dfrac{1}{6}x=\dfrac{2}{3}+3=\dfrac{11}{3}\\ x=\dfrac{11}{3}:\dfrac{1}{6}=22\\ TH2:\dfrac{1}{6}x-3=-\dfrac{2}{3}\\ \dfrac{1}{6}x=-\dfrac{2}{3}+3=\dfrac{7}{3}\\ x=\dfrac{7}{3}:\dfrac{1}{6}=14\)

|5-4x|=3-x
=>|4x-5|=3-x
=>\(\left\{{}\begin{matrix}3-x>=0\\\left(4x-5\right)^2=\left(3-x\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =3\\\left(4x-5-x+3\right)\left(4x+5+x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =3\\\left(3x-2\right)\left(5x+2\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{2}{3};-\dfrac{2}{5}\right\}\)
\(\left|6-3x\right|=6+x\)
=>|3x-6|=x+6
=>\(\left\{{}\begin{matrix}x+6>=0\\\left(3x-6\right)^2=\left(x+6\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-6\\\left(3x-6-x-6\right)\left(3x-6+x+6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-6\\4x\left(2x-12\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{0;6\right\}\)
|4-x|=6
=>|x-4|=6
=>\(\left[{}\begin{matrix}x-4=6\\x-4=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
|3-x|=8
=>|x-3|=8
=>\(\left[{}\begin{matrix}x-3=8\\x-3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-5\end{matrix}\right.\)
|4-x|=2-x
=>|x-4|=2-x
=>\(\left\{{}\begin{matrix}2-x>=0\\\left(x-4\right)^2=\left(2-x\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =2\\\left(x-4-2+x\right)\left(x-4+2-x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =2\\\left(2x-6\right)\cdot\left(-2\right)=0\end{matrix}\right.\)
=>\(x\in\varnothing\)
|3+2x|=2x+5
=>|2x+3|=2x+5
=>\(\left\{{}\begin{matrix}2x+5>=0\\\left(2x+5\right)^2=\left(2x+3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{5}{3}\\4x^2+20x+25=4x^2+12x+9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{5}{3}\\20x+25=12x+9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{5}{3}\\x=-2\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

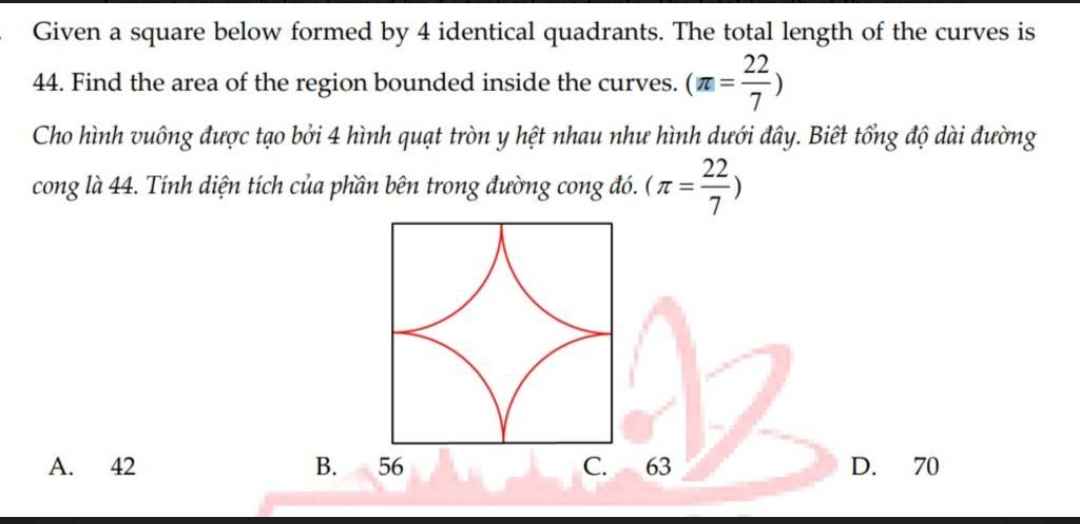
Độ dài 1 đường cong là:
$44:4=11$ (đvi độ dài)
Chu vi bốn hình quạt tròn là:
$11\times4=44$ (đvi độ dài)
Từ bốn hình quạt tròn đó ta ghép được 1 hình tròn. Khi đó:
Độ dài cạnh hình vuông là:
$44:\frac{22}{7}=14$ (đvi độ dài)
Diện tích hình vuông là:
$14\times14=196$ (đvi diện tích)
Diện tích bốn hình quạt tròn là:
$\frac{14}{2}\times\frac{14}{2}\times\frac{22}{7}=154$ (đvi diện tích)
Diện tích của phần bên trong đường cong là:
$196-154=42$ (đvi diện tích)
4 curves form 1 circle
The radius of the circle is:
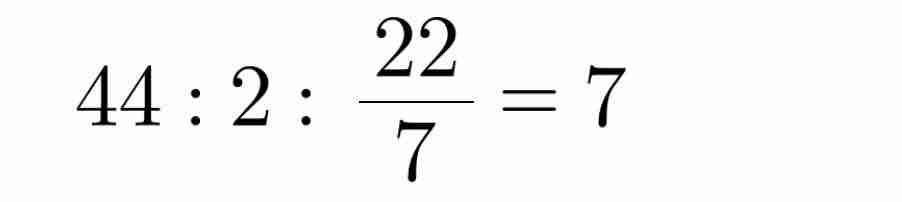 The area of the circle is:
The area of the circle is:
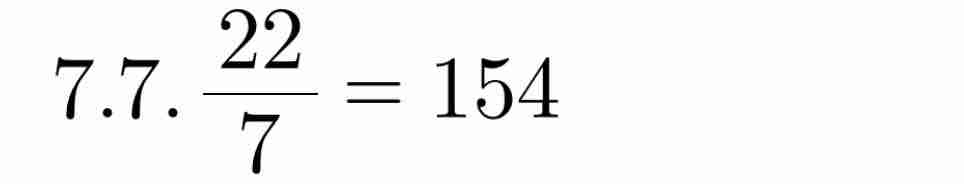 The length of the side of the square is:
The length of the side of the square is:
7.2 = 14
The area of the square is:
14.14 = 196
The area of the region bounded inside the curves is:
196 - 154 = 42

Bài 1
a: ĐKXĐ: \(n\ne4\)
Để A nguyên thì \(3n+9⋮n-4\)
=>\(3n-12+21⋮n-4\)
=>\(21⋮n-4\)
=>\(n-4\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{5;3;7;1;11;-3;25;-17\right\}\)
b: ĐKXĐ: n<>1/2
Để B nguyên thì \(6n+5⋮2n-1\)
=>\(6n-3+8⋮2n-1\)
=>\(8⋮2n-1\)
mà 2n-1 lẻ(do n nguyên)
nên \(2n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{1;0\right\}\)
Bài 2:
a: \(\left|x-\dfrac{1}{2}\right|>=0\forall x\)
=>\(-\dfrac{1}{2}\left|x-2\right|< =0\forall x\)
=>\(A=-\dfrac{1}{2}\left|x-2\right|+\dfrac{3}{2}< =\dfrac{3}{2}\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
b: \(\left|\dfrac{1}{2}-x\right|>=0\forall x\)
=>\(-2,3\left|\dfrac{1}{2}-x\right|< =0\forall x\)
=>\(D=-2,3\left|\dfrac{1}{2}-x\right|+2< =2\forall x\)
Dấu '=' xảy ra khi 1/2-x=0
=>x=1/2
Bài 1:
\(A=\dfrac{3n+9}{n-4}=\dfrac{3n-12}{n-4}+\dfrac{21}{n-4}=3+\dfrac{21}{n-4}\)
Để A nguyên thì \(\dfrac{21}{n-4}\) phải nguyên hay \(\left(n-4\right)\inƯ\left(21\right)=\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
\(\Rightarrow n\in\left\{5;3;7;1;11;-3;25;-17\right\}\) (thoả mãn điều kiện)
Vậy...
\(B=\dfrac{6n+5}{2n-1}=\dfrac{6n-3}{2n-1}+\dfrac{8}{2n-1}=3+\dfrac{8}{2n-1}\)
Để B nguyên thì \(\dfrac{8}{2n-1}\) phải nguyên hay \(\left(2n-1\right)\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
Mặt khác: Vì n nguyên nên 2n-1 là số lẻ
Do đó: \(\left(2n-1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow n\in\left\{1;0\right\}\)
Vậy....

|3x+4|=x+2
=>\(\left\{{}\begin{matrix}x+2>=0\\\left(3x+4\right)^2=\left(x+2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\\left(3x+4-x-2\right)\left(3x+4+x+2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\\left(2x+2\right)\left(4x+6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\x\in\left\{-1;-\dfrac{3}{2}\right\}\end{matrix}\right.\Leftrightarrow x\in\left\{-1;-\dfrac{3}{2}\right\}\)
|5x-6|=4-x
=>\(\left\{{}\begin{matrix}4-x>=0\\\left(5x-6\right)^2=\left(4-x\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =4\\\left(5x-6-4+x\right)\left(5x-6+4-x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =4\\\left(6x-10\right)\left(4x-2\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{5}{3};\dfrac{1}{2}\right\}\)
|5-2x|=x-3
=>|2x-5|=x-3
=>\(\left\{{}\begin{matrix}x-3>=0\\\left(2x-5\right)^2=\left(x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=3\\\left(2x-5\right)^2-\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=3\\\left(2x-5-x+3\right)\left(2x-5+x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=3\\\left(x-2\right)\left(3x-8\right)=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
|3-2x|=6+4x
=>|2x-3|=4x+6
=>\(\left\{{}\begin{matrix}4x+6>=0\\\left(4x+6\right)^2=\left(2x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{3}{2}\\\left(4x+6-2x+3\right)\left(4x+6+2x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{3}{2}\\\left(2x+9\right)\left(6x+3\right)=0\end{matrix}\right.\Leftrightarrow x=-\dfrac{1}{2}\)
|6-3x|=3x
=>|3x-6|=3x
=>|x-2|=x
=>\(\left\{{}\begin{matrix}x>=0\\\left(x-2\right)^2=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=0\\-4x+4=0\end{matrix}\right.\Leftrightarrow x=1\)

\(\left|3x+4\right|=x+2\\ \Rightarrow\left[{}\begin{matrix}3x+4=x+2\left(x\ge-\dfrac{4}{3}\right)\\3x+4=-\left(x+2\right)\left(x< -\dfrac{4}{3}\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x-x=2-4\\3x+x=-2-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=-2\\4x=-6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-1\left(tm\right)\\x=-\dfrac{6}{4}=-\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
______________________
\(\left|5x-6\right|=4-x\\ \Rightarrow\left[{}\begin{matrix}5x-6=4-x\left(x\ge\dfrac{6}{5}\right)\\5x-6=-\left(4-x\right)\left(x< \dfrac{6}{5}\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}5x+x=4+6\\5x-x=-4+6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}6x=10\\4x=2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{10}{6}=\dfrac{5}{3}\left(tm\right)\\x=\dfrac{2}{4}=\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
________________________
\(\left|5-2x\right|=x-3\\ \Rightarrow\left[{}\begin{matrix}5-2x=x-3\left(x\le\dfrac{5}{2}\right)\\5-2x=-\left(x-3\right)\left(x>\dfrac{5}{2}\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}-2x-x=-3-5\\-2x+x=3-5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}-3x=-8\\-x=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{-8}{-3}=\dfrac{8}{3}\left(ktm\right)\\x=2\left(ktm\right)\end{matrix}\right.\)
\(\left|3-2x\right|=6+4x\\ \Rightarrow\left[{}\begin{matrix}3-2x=6+4x\left(x\le\dfrac{3}{2}\right)\\3-2x=-\left(6+4x\right)\left(x>\dfrac{3}{2}\right)\end{matrix}\right.\\\Rightarrow\left[{}\begin{matrix}4x+2x=3-6\\-2x+4x=-6-3\end{matrix}\right. \\ \Rightarrow\left[{}\begin{matrix}6x=-3\\2x=-9\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\left(tm\right)\\x=-\dfrac{9}{2}\left(ktm\right)\end{matrix}\right.\)
________________________
\(\left|6-3x\right|=3x\\ \Rightarrow\left[{}\begin{matrix}6-3x=3x\left(x\le2\right)\\6-3x=-3x\left(x>2\right)\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x+3x=6\\6=0\left(ktm\right)\end{matrix}\right.\\ \Rightarrow x=\dfrac{6}{6}=1\left(tm\right)\)

Số công nhân cần có để hoàn thành công việc trong 14 ngày là:
\(56\cdot\dfrac{21}{14}=56\cdot\dfrac{3}{2}=84\left(người\right)\)
Số công nhân cần tăng thêm là:
84-56=28(người)
Giải:
Một công nhân hoàn thành công việc đó trong số ngày là:
21 x 56 = 1176 (ngày)
Để hoàn thành công việc trong 14 ngày cần số người là:
1176 : 14 = 84 (người)
Vậy để hoàn thành công việc trong 14 ngày cần bổ sung thêm số người là:
84 - 56 = 28 (người)
Đáp số:.....
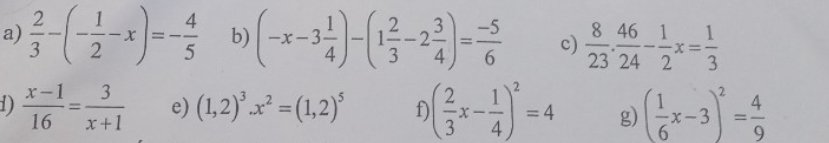
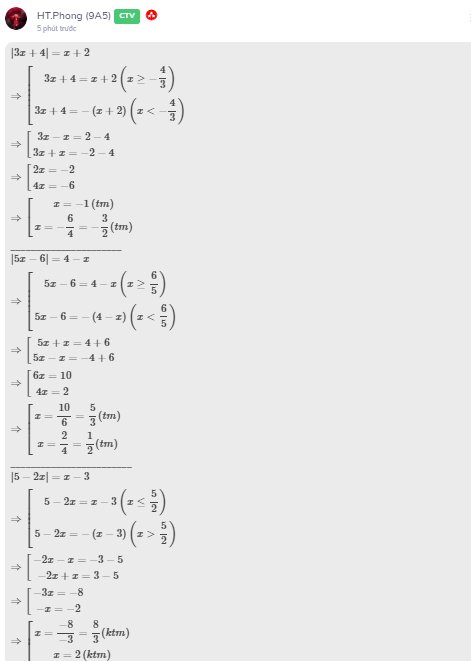
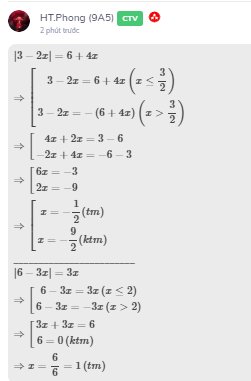


Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\b=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}\\ =\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(1\right)\)
\(VP=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{bd\cdot k^2}{bd}=k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)