Trong 2 ngày với 8 người thì sửa được 64m đường. Vậy trong 5 ngày với 9 người thì sửa được bao nhiêu mét đường?(Năng suất của mỗi người đều như nhau)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(72.121+27.121+121\\ =121.\left(72+27+1\right)\\ =121.100=12100\)
b) \(2724-\left(2^3.3^2-2^4.3\right)\\ =2724-\left(8.9-16.3\right)\\ =2724-\left(72-48\right)\\ =2724-24=2700\)
c) \(47-\left(45.2^4-5^2.12\right):4\\ =47-\left(45.16-25.12\right):4\\ =47-\left(720-300\right):4\\ =47-420:4\\ =47-105=-58\)
d) Số số hạng dãy trên là:
( 100 - 1 ) : 3 + 1 = 34 (số hạng)
Tổng dãy trên là:
(100 + 1) . 34 : 2 = 1717
Vậy: 100 + 97 + 94 + ... + 4 + 1 = 1717

a: \(\widehat{x'Oy'}+\widehat{x'Oy}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oy'}+120^0=180^0\)
=>\(\widehat{x'Oy'}=60^0\)
Ta có: OA là phân giác của góc x'Oy'
=>\(\widehat{x'OA}=\widehat{y'OA}=\dfrac{\widehat{x'Oy'}}{2}=30^0\)
Ta có: \(\widehat{y'OA}+\widehat{y'OB}=30^0+150^0=180^0\)
=>A,O,B thẳng hàng
b: Ta có: \(\widehat{xOB}=\widehat{x'OA}\)(hai góc đối đỉnh)
mà \(\widehat{x'OA}=30^0\)
nên \(\widehat{xOB}=30^0\)
=>\(\widehat{xOB}=\dfrac{1}{2}\cdot\widehat{xOy}\)
=>OB là phân giác của góc xOy

Đặt: \(S=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+\dfrac{5^2}{11.16}+...+\dfrac{5^2}{26.31}\)
\(\Rightarrow\dfrac{S}{5}=\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+...+\dfrac{5}{26.31}\\ =1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{26}-\dfrac{1}{31}\\ =1-\dfrac{1}{31}=\dfrac{30}{31}\\ \Rightarrow S=\dfrac{30}{31}.5=\dfrac{150}{31}\)
Sửa bài:
Đặt biểu thức là A. ta được:
\(\dfrac{A}{5}=\dfrac{5}{1.6}+\dfrac{5}{6.11}+...+\dfrac{5}{26.31}\\ \dfrac{A}{5}=1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\\ \dfrac{A}{5}=\dfrac{30}{31}\\ A=\dfrac{150}{31}.\)

\(12:\dfrac{6}{5}=12\times\dfrac{5}{6}=\dfrac{12\times5}{6}\\ =\dfrac{6\times2\times5}{6}=2\times5=10\)

\(3\left(x-2\right)=-100+211\\ 3\left(x-2\right)=111\\ x-2=37\\ x=39.\)
`#3107.101107`
`3(x - 2) = -100 + 211`
`\Rightarrow 3(x - 2) = 111`
`\Rightarrow x - 2 = 111 \div 3`
`\Rightarrow x - 2 = 37`
`\Rightarrow x = 37 + 2`
`\Rightarrow x = 39`
Vậy, `x = 39.`

Vì 1200 > 900
Vậy góc có số đó 1120 là góc tù.

gọi tuổi cô giáo là x
tuổi trung bình 20HS là y
theo đề ta có: \(y=\dfrac{x}{2}\) (1)
tuổi trung bfinh của 20HS và cô giáo mà nhỏ hơn cô giáo 20 tuổi là:
\(\dfrac{20y+x}{21}=x-20\) (2)
từ (1) (2) =>
\(\dfrac{20\cdot\dfrac{x}{2}+x}{21}=x-20\\ \dfrac{10x+x}{21}=x-20\\ \dfrac{11x}{21}=x-20\\ 11x=21x-420\\ 420=21x-11x\\ 420=10x\\ x=42\)
vậy số tuổi cô giáo là 42 tuổi

\(y:84=\dfrac{106}{84}\\ y=\dfrac{106}{84}\times84\\ y=106.\)
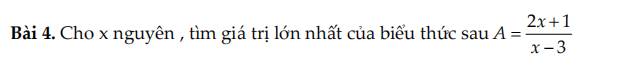 giúp em với ạ , em cảm ơn ạ
giúp em với ạ , em cảm ơn ạ
Đây là toán nâng cao ba đại lượng tỉ lệ thuận, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Một người một ngày sửa được số mét đường là:
64 : 8 : 2 = 4 (m)
Trong 5 ngày 9 người với năng suất làm như thế thì sẽ được số mét đường là:
4 x 9 x 5 = 180 (m)
Đáp số: 180 m