
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thi không giúp được bạn nhé!
Mà có giúp cũng đâu có bài đâu mà giúp ^^

\(\left(2-x\right)^{24}=\left(x-2\right)^{24}=\sum\limits^{24}_{k=0}C^k_{24}.x^k.\left(-2\right)^{24-k}\)
b) Hệ số tổng quát là \(a_k=C^k_{24}\left(-2\right)^{24-k}\) \(\Rightarrow a_9=C^9_{24}.\left(-2\right)^{24-9}=-2^{15}.C^9_{24}\) -> Sai
c) SHTQ: \(T_k=C^k_{24}.x^k.\left(-2\right)^{24-k}\)
\(x^{20}\Rightarrow k=20\) \(\Rightarrow T_4=C^{20}_{24}.x^{20}\left(-2\right)^{24-20}=170016x^{20}\) -> Sai
SHTQ trong khai triển \(\left(2-x\right)^{24}\) là: \(C_{24}^k.\left(-x\right)^k.2^{24-k}=C_{24}^k.\left(-1\right)^k.2^{24-k}.x^k\)
b.
Số hạng chứa \(x^9\Rightarrow k=9\)
\(\Rightarrow a_9=C_{24}^9.\left(-1\right)^9.2^{24-9}=-C_{24}^9.2^{15}\)
c.
Số hạng chứa \(x^{20}\Rightarrow k=20\)
Số hạng đó là:
\(C_{24}^{20}.\left(-1\right)^{20}.2^{24-20}.x^{20}=C_{24}^{20}.2^4.x^{20}=170016.x^{20}\)


Chọn 4 chữ số còn lại: có \(C_6^4\) cách
Chọn 4 chữ số còn lại sao cho có mặt chữ số 0: có \(C_5^3\) cách
Hoán vị 6 chữ số: \(6!\) cách
Hoán vị 6 chữ số sao cho chữ số 0 đứng đầu: \(5!\) cách
\(\Rightarrow C_6^4.6!-C_5^3.5!\) số thỏa mãn

Đường tròn (C) tâm \(I\left(-1;1\right)\) bán kính \(R=\sqrt{17}\)
\(y=-2x+2017\Leftrightarrow2x+y-2017=0\)
Tiếp tuyến vuông góc d nên nhận \(\left(1;-2\right)\) là 1 vtpt
Gọi tiếp tuyến là d' thì pt d' có dạng: \(x-2y+c=0\)
Do d' là tiếp tuyến của (C) nên: \(d\left(I;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|-1-2.1+c\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{17}\)
\(\Leftrightarrow\left|c-3\right|=\sqrt{85}\Rightarrow c=3\pm\sqrt{85}\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}x-2y+3+\sqrt{85}=0\\x-2y+3-\sqrt{85}=0\end{matrix}\right.\)

a: Số cách chọn 6 viên bi đỏ là \(C^6_{12}\left(cách\right)\)
Số cách chọn 6 viên bi vàng là \(C^6_8\left(cách\right)\)
=>Tổng số cách chọn 6 viên bi mà chỉ có 1 màu là \(C^6_{12}+C^6_8=952\left(cách\right)\)
Số cách chọn 6 viên bi bất kì là \(C^6_{20}=38760\left(cách\right)\)
Xác suất là \(\dfrac{952}{38760}=\dfrac{7}{285}\)
b: TH1: 5 đỏ, 1 vàng
=>Số cách chọn là \(C^5_{12}\cdot C^1_8=6336\left(cách\right)\)
TH2: 6 đỏ
=>Số cách chọn là \(C^6_{12}=924\left(cách\right)\)
Xác suất để chọn 6 viên bi, trong đó số viên bi đỏ nhiều hơn 4 là \(\dfrac{6336+924}{C^6_{20}}=\dfrac{121}{646}\)
=>Xác suất để chọn 6 viên bi, trong đó số viên bi đỏ ít hơn hoặc bằng 4 là \(1-\dfrac{121}{646}=\dfrac{525}{646}\)
c: Số cách chọn 6 viên bi mà trong đó không có viên màu vàng nào là \(C^6_{12}\left(cách\right)\)
=>Số cách chọn 6 viên bi mà trong đó có ít nhất 1 viên màu vàng là \(C^6_{20}-C^6_{12}=37836\left(cách\right)\)
=>Xác suất là \(\dfrac{37836}{C^6_{20}}=\dfrac{3153}{3230}\)
d: Số cách chọn 6 viên bi sao cho không có đủ 2 màu là \(C^6_8+C^6_{12}=952\left(cách\right)\)
=>Số cách chọn 6 viên bi sao cho có đủ 2 màu là \(C^6_{20}-952=37808\left(cách\right)\)
=>Xác suất là \(\dfrac{37808}{C^6_{20}}=\dfrac{278}{285}\)
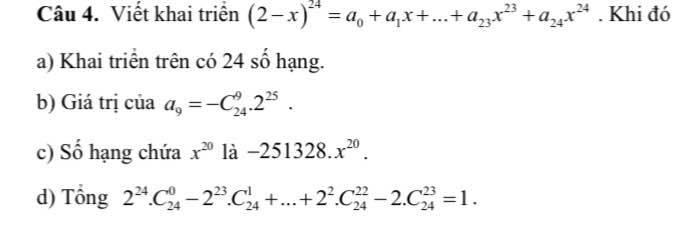
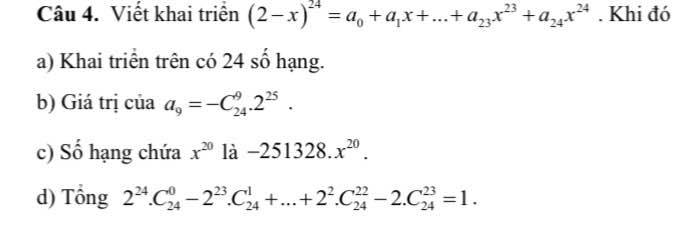
Câu 1: D
Câu 2: C
Câu 3: Thay x=1 và y=2 vào y=4x+m-1, ta được:
\(m-1+4\cdot1=2\)
=>m+3=2
=>m=-1
=>Chọn B
Câu 4: B
Câu 5: Hoành độ đỉnh là:
\(x=-\dfrac{b}{2a}=\dfrac{-\left(-6\right)}{2\cdot\left(-2\right)}=\dfrac{6}{-4}=-\dfrac{3}{2}\)
=>Chọn C
Câu 6:
Phương trình hoành độ giao điểm là:
\(x^2-4x=-x-2\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Thay x=1 vào y=-x-2, ta được:
y=-1-2=-3
Thay x=2 vào y=-x-2, ta được:
y=-2-2=-4
=>Chọn D
Câu 7: A
Câu 8: \(f\left(x\right)=-2x^2+8x-8\)
\(=-2\left(x^2-4x+4\right)\)
\(=-2\left(x-2\right)^2< =0\forall x\)
=>Chọn C
Câu 9: \(x^4-5x^2+4< 0\)
=>\(\left(x^2-1\right)\left(x^2-4\right)< 0\)
=>\(1< x^2< 4\)
=>\(\left[{}\begin{matrix}1< x< 2\\-2< x< -1\end{matrix}\right.\)
=>Chọn D
Câu 10:
ĐKXĐ: \(x\in R\)
\(x^2-x+2=2x^2-4x+4\)
=>\(-x^2+3x-2=0\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
=>Chọn B