Cho ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB< BC, CD và AD. Chứng minh rằng:
a) AMPD là hình bình hành
b) AN song song với CQ
c) MNPQ là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3x^3-14x^2+4x+3\)
\(=\left(3x^3-15x^2+9x\right)+\left(x^2-5x+3\right)\)
\(=3x\left(x^2-5x+3\right)+\left(x^2-5x+3\right)\)
\(=\left(3x+1\right)\left(x^2-5x+3\right)\)

\(\left(5x+1\right)^2-\left(2xy-3\right)^2\\ =\left[\left(5x+1\right)-\left(2xy-3\right)\right]\left[\left(5x+1\right)+\left(2xy-3\right)\right]\\ =\left(5x+1-2xy+3\right)\left(5x+1+2xy-3\right)\\ =\left(5x-2xy+4\right)\left(5x+2xy-2\right)\)
(5\(x\) + 1)2 - (2\(xy\) - 3)2
= [(5\(x\) + 1) - (2\(xy\) - 3)].[(5\(x\) + 1) + (2\(xy\) - 3)]
= [ 5\(x\) + 1 - 2\(xy\) + 3][5\(x\) + 1 + 2\(xy\) - 3]
= [5\(x\) - 2\(xy\) + (1 + 3)][5\(x\) + 2\(xy\) - (3 - 1)]
= [5\(x\) - 2\(x\)\(y\) + 4][5\(x+2xy\) - 2]

d1 // d2 ⇔ 3 - m = - 6 + 2m
2m + m = 3 + 6
3m = 9
m = 9 : 3
m = 3 (loại)
không có gía trị nào của m ≠ 3 thoả mãn đề bài

\(P=\left(2x-y\right)^2-\left(6x-3y\right)^2-\left|x+y-9\right|+2023\)
\(=\left(2x-y\right)^2-9\left(2x-y\right)^2-\left|x+y-9\right|+2023\)
\(=-8\left(2x-y\right)^2-\left|x+y-9\right|+2023< =2023\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}2x-y=0\\x+y-9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x\\x+y=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=6\\x=3\end{matrix}\right.\)

a,b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{BMA}=\widehat{CMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMBA=ΔMCD
=>AB=CD
mà AB<AC
nên CD<AC
c: ΔMBA=ΔMCD
=>\(\widehat{MAB}=\widehat{MDC}\left(1\right)\)
Xét ΔCDA có CD<CA
mà \(\widehat{CAD};\widehat{CDA}\) lần lượt là góc đối diện của các cạnh CD,CA
nên \(\widehat{CAD}< \widehat{CDA}\)(2)
Từ (1),(2) suy ra \(\widehat{CAD}< \widehat{MAB}\)

2x³ - 5x² + 8x - 3
= 2x³ - x² - 4x² + 2x + 6x - 3
= (2x³ - x²) - (4x² - 2x) + (6x - 3)
= x²(2x - 1) - 2x(2x - 1) + 3(2x - 1)
= (2x - 1)(x² - 2x + 3)

Do là bài tập cũng gọi là dành cho chuyên hơi khó xíu bt học thêm ấy chỗ ẫy cũng khó nên bài tập ít nhưng mà nâng cao
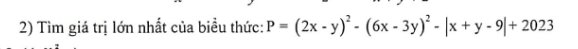
a: ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DP=PC=\dfrac{DC}{2}\)
mà AB=DC
nên AM=MB=DP=PC
Ta có: \(AQ=QD=\dfrac{AD}{2}\)
\(BN=NC=\dfrac{BC}{2}\)
mà AD=BC
nên AQ=QD=BN=NC
Xét tứ giác AMPD có
AM//PD
AM=PD
Do đó: AMPD là hình bình hành
b: Xét tứ giác ANCQ có
AQ//CN
AQ=CN
Do đó: ANCQ là hình bình hành
=>AN//CQ
c: Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
=>BD cắt MP tại trung điểm của mỗi đường(1)
Ta có: ANCQ là hình bình hành
=>AC cắt NQ tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(3)
Từ (1),(2),(3) suy ra MP cắt NQ tại trung điểm của mỗi đường
=>MNPQ là hình bình hành
ai giúp ko