Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lời giải:
Số hsg là: $32.\frac{1}{4}=8$ (hs)
Số hsk là: $(32-8).\frac{3}{8}=9$ (hs)
Số hstb là: $32-8-9=15$ (hs)

81975 = (84)493.83 = \(\overline{..6}\)493. \(\overline{...2}\) = \(\overline{..2}\)

Lời giải:
a. $A=3xy(x^2+2xy+y^2)=3xy(x+y)^2=3.\frac{1}{2}.\frac{-1}{3}(\frac{1}{2}+\frac{-1}{3})^2=\frac{-1}{72}$
b.
$B=(-1)^2.3^2+(-1).3+(-1)^3+3^3=32$
c.
$D=5^2+4.5.1-3.1^3=42$
d.
$D=2xy(x+y)=2.1(-3)(1-3)=12$
e.
$M=\frac{(x+2)(2x-1)}{x+2}=2x-1=2(-1)-1=-3$

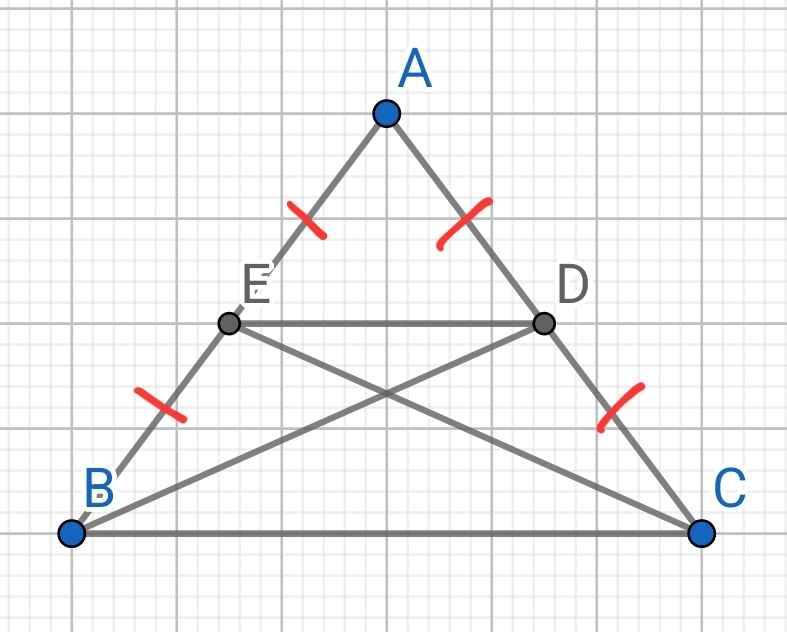
a) Do BD là đường trung tuyến của ∆ABC
⇒ D là trung điểm AC
⇒ AD = AC/2
Do CE là đường trung tuyến của ∆ABC
⇒ E là trung điểm AB
⇒ AE = AB/2
Mà AB = AC (∆ABC cân tại A)
⇒ AD = AC/2 = AB/2 = AE
⇒ ∆ADE cân tại A
b) Do ∆ADE cân tại A (cmt)
⇒ ∠AED = ∠ADE = (180⁰ - ∠BAC)/2
Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC)/2
⇒ ∠AED = ∠ABC = (180⁰ - ∠BAC)/2
Mà ∠AED và ∠ABC là hai góc đồng vị
⇒ ED // BC
∆ABC cân tại A
⇒ ∠ABC = ∠ACB (hai góc ở đáy)
⇒ ∠EBC = ∠DCB
Tứ giác BCDE có:
ED // BC (cmt)
⇒ BCDE là hình thang
Mà ∠EBC = ∠DCB (cmt)
⇒ BCDE là hình thang cân

(7/111 - 4/33 + 9/37).(1/2 - 1/3 -1/6)
= (7/111 - 4/33 + 9/37).0
= 0

60 ⋮ 15
⇒ 60n ⋮ 15
45 ⋮ 15
⇒ (60n + 45) ⋮ 15 (1)
60 ⋮ 2
⇒ 60n ⋮ 2
45 không chia hết cho 2
⇒ (60n + 45) không chia hết cho 2 (2)
Từ (1) và (2) ⇒ (60n + 45) không chia hết cho 30
Vậy (60n + 45) chia hết cho 15 nhưng (60n + 45) không chia hết cho 30
Lời giải:
$60n+45=15(4n+3)\vdots15$
$60n+45=30(2n+1)+15\not\vdots 30$ do $15\not\vdots 30$
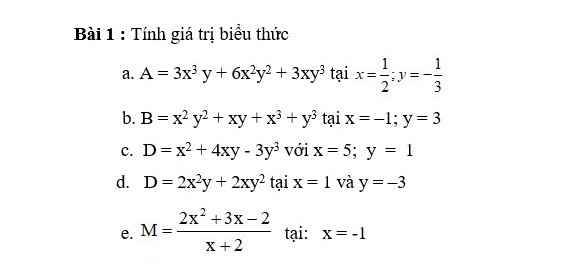
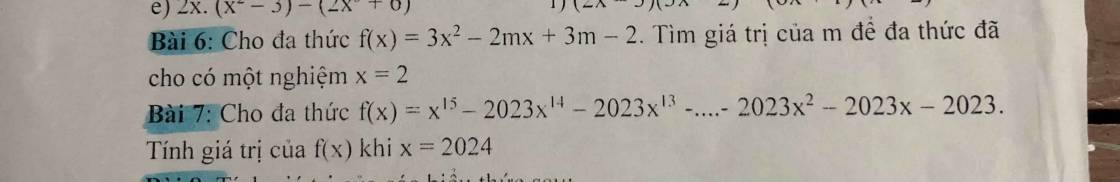


1.
$3x^4-48=3(x^4-16)=3[(x^2)^2-4^2]=3(x^2-4)(x^2+4)$
$=3(x-2)(x+2)(x^2+4)$
2.
$x^3-4x^2+8x-8=(x^3-8)-(4x^2-8x)$
$=(x-2)(x^2+2x+4)-4x(x-2)=(x-2)(x^2+2x+4-4x)=(x-2)(x^2-2x+4)$
3.
$x^4-27x=x(x^3-27)=x(x^3-3^3)=x(x-3)(x^2+3x+9)$
4.
$x^4-x^3+x^2-1=(x^4-x^3)+(x^2-1)=x^3(x-1)+(x-1)(x+1)$
$=(x-1)(x^3+x+1)$
5.
$x^5+x^3-x^2-1=(x^5+x^3)-(x^2+1)=x^3(x^2+1)-(x^2+1)$
$=(x^2+1)(x^3-1)=(x^2+1)(x-1)(x^2+x+1)$
6.
$x^3+2x^2+2x+1=(x^3+x^2)+(x^2+2x+1)=x^2(x+1)+(x+1)^2$
$=(x+1)(x^2+x+1)$
7.
$x^3+x^2-4x-4=(x^3+x^2)-(4x+4)=x^2(x+1)-4(x+1)$
$=(x+1)(x^2-4)=(x+1)(x-2)(x+2)$
8.
$x^4-2x^3+2x-1=(x^4-2x^3+x^2)-(x^2-2x+1)$
$=(x^2-x)^2-(x-1)^2=x^2(x-1)^2-(x-1)^2=(x-1)^2(x^2-1)=(x-1)^2(x-1)(x+1)$