Câu hỏi của Lê Tài Bảo Châu ( Team HP ) - Toán lớp 7 - Học toán với OnlineMath

Bạn tham khảo link này nhé!

ĐÁP ÁN: 2/651

#Hình bạn tự vẽ nhé!!!#

a)Ta có: AM=DM(M là trung điểm của AD); BN=CN(N là trung điểm của BC)

\(\Rightarrow\)MN là đường trung bình của hình thang ABCD

\(\Rightarrow MN//CD\left(1\right)\)

Ta lại có:AM=DM(cmt); AE=CE(E là trung điểm của AC)

\(\Rightarrow\)ME là đường trung bình của \(\Delta ACD\)

\(\Rightarrow ME//CD\left(2\right)\)

Từ(1) và (2), suy ra:\(MN\equiv ME\)(theo tiên đề Ơ-clit)

                           \(\Rightarrow M,N,E\) thẳng hàng (3)    

Vì BN=CN(cmt); BF=DF(F là trung điểm của BD)

\(\Rightarrow\)NF là đường trung bình của \(\Delta BCD\)

\(\Rightarrow NF//CD\left(4\right)\)

Từ(1) và (4), suy ra:\(MN\equiv NF\)(theo tiên đề Ơ-clit)

                           \(\Rightarrow M,N,F\)  thẳng hàng(5)

Từ (2) và (5), suy ra:M,N,P,Q thẳng hàng

a) +)Xét hình thang ABCD có: M là trug điểm AD, N là trung điểm BC

=> MN là đường trung bình hình thang ABCD

=> MN//AB//DC (1)

+) xét tam giác ADC có: M là trung điểm AD; E là trung điểm EC

=> ME là đường trung bình tam giác ADC

=> ME//=1/2 DC (2)

+) Xét tam giác ADB có M là trung điểm AD, F là trung điểm DB 

=> MF là đường trung bình của tam giác ADB

=> MF//=1/2 AB (3)

Từ (1), (2), (3) suy ra MN, ME, MF cùng nằm trên một đường thẳng

=> M, N, E, F thẳng hàng 

b) 

Ta có: \(EF=ME-MF=\frac{1}{2}DC-\frac{1}{2}AB=\frac{DC-AB}{2}\)

a) 5.(x^2-3x+1)+x.(1-5x)=x-2

\(\Leftrightarrow5x^2-15x+5+x-5x^2=x-2\)

\(\Leftrightarrow-14x-x=-2-5\)

\(\Leftrightarrow-15x=-7\)

\(\Leftrightarrow x=\frac{7}{15}\)

b\(,3x.\left(\frac{4}{3}+1\right)-4x\left(x-2\right)=10\)

\(\Leftrightarrow4x+3x-4x^2+8x-10=0\)

\(\Leftrightarrow-4x^2+15x-10=0\)

Đề sai???

\(c,12x^2-4x\left(3x-5\right)=10x-17\)

\(\Leftrightarrow12x^2-12x^2+20x-10x=-17\)

\(\Leftrightarrow10x=-17\)

\(\Leftrightarrow x=-\frac{17}{10}\)

\(d,4x\left(x-5\right)-7x\left(x-4\right)+3x^2=12\)

\(\Leftrightarrow4x^2-20x-7x^2+28x+3x^2=12\)

\(\Leftrightarrow8x=12\)

\(\Leftrightarrow x=\frac{3}{2}\)

\(a,5\left(x^2-3x+1\right)+x\left(1-5x\right)=x-2\)

\(\Leftrightarrow5x^2-15x+5+x-5x^2-x+2=0\)

\(\Leftrightarrow-15x+7=0\)

\(\Leftrightarrow-15x=-7\)

\(\Leftrightarrow x=-\frac{7}{-15}\)

\(\Leftrightarrow x=\frac{7}{15}\)

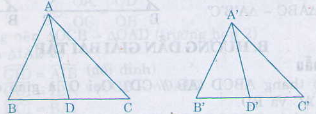
Xét ∆A’B’D’ và ∆ABD có:

ˆB = ˆB′

ˆBAD = ˆB′A′D′

=> ∆A’B’D’∽ ∆ABD theo tỉ số K = A′B′/AB= A′D′AD

Mà  ∆A’B’C’ ∽ ∆ABC theo tỉ số = A′B′/AB

=> A′D′/AD

 = k

Gọi AD và A'D' lần lượt là hai đường phân giác của tam giác ABC và A'B'C'

Xét ∆A’B’D’ và ∆ABD có:

B=B' 

BAD =B'A'D'

=> ∆A’B’D’ ∽ ∆ABD =>\(\frac{AB}{A'B'}\)=\(\frac{AD}{A'D'}\)=k

Mà  ∆A’B’C’ ∽ ∆ABC theo tỉ số \(\frac{AB}{A'B'}\)

=> \(\frac{AD}{A'D'}\)=k

Gọi vận tốc dự định của ô tô là x ( >5 , km/h)

Thời gian dự định ô tô đến B: 11h 30 p-7h=4 h 30 p=4,5 ( giờ)

Quãng đường đi dự định là: 4,5 x ( km)

Vận tốc thực tế ô tô đi là: x-5 (km/h)

Thời gian thực tế ô tô đi là: 12h -7h=5 ( giờ)

Quãng đường đi đc thực tế là: 5(x-5) (km)

Vì quãng được thực tế hay dự định đều bằng quãng đường AB. Nên ta có phương trình:

5(x-5)=4,5 x

<=> 5x-25=4,5x

<=> 0,5x=25

<=> x=50 

Vậy quãng đường AB là: 4,5.50=225 (km)

thanks

2xy+x²y⁴ +1

=2x³ y⁵ +1

=3x³y⁵

cho a 1

L.I.K.E

để a 

làm hộ bn này bài này nào 

a² - b² - 2a + 1

= (a - 1)² - b²

= (a - 1 + b)(a - 1 - b)

\(a^2-b^2-2a+1=a^2-2a+1-b^2\)

                                  \(=\left(a-1\right)^2-b^2=\left(a-1-b\right)\left(a-1+b\right)\)