l x-9 l + l 2-xl =7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số kg sắt quặng A :
\(80x\dfrac{40}{100}=32\left(kg\right)\)
Tổng số kg sắt quặng B :
\(32+20=52\left(kg\right)\)
Tổng số kg quặng B gồm cả sắt :
\(80+20=100\left(kg\right)\)
Phần trăm sắt quặng B :
\(\dfrac{52}{100}x100\%=52\%\)
Đáp số : \(52\%\)
Quặng B nặng số kg là:
`80 + 20= 100 (kg)`
Nung `80`kg quặng A thu được số kg sắt là:
`80 : 100` x `40 = 32 (kg)`
Số kg sắt có trong quặng B là:
`32+ 20 = 52 (kg)`
Quặng B chứa % sắt là:
`52 : 100 ` x `100 = 52`% (sắt)
Đáp số: ....
tìm số tự nhiên a < hoặc = 185, biết rằng khi chia a cho số từ nhiên b thì được thương là 4 và dư 35


A và B chia hết cho C
Ta có:
\(\dfrac{A}{C}=\dfrac{12x^{2n}y^{12-3n}}{3x}=4x^{2n-1}y^{12-3n}\)
\(\dfrac{B}{C}=\dfrac{x^3y^7}{3x}=\dfrac{1}{3}x^2y^7\)
Để A và B chia hết cho C thì: \(\left\{{}\begin{matrix}2n-1\ge0\\12-3n\ge0\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}\le n\le4\)
Mà: n thuộc Z => n ∈ {1; 2; 3; 4}

Số kg quặng B thu được xong khi nung nóng 80kg quặng A và 20kg sắt là:
\(80+20=100\left(kg\right)\)
Số kg sắt có trong 80kg quặng A là:
\(80\times40\%=32\left(kg\right)\)
Số kg sắt có trong 100kg quặng B là:
\(32+20=52\left(kg\right)\)
Quặng B có số phần trăm sắt là:
\(52:100\times100=52\left(\%\right)\)
Đáp số: 52% sắt

Gọi 2 số cần tìm là \(\overline{5ab};\overline{3cd}\) theo đề bài
\(\overline{5ab}+\overline{3cd}=836\)
\(500+\overline{ab}+300+\overline{cd}=836\)
\(\Rightarrow\overline{ab}+\overline{cd}=36\)
Đến đây là dạng toán tìm 2 số khi biết tổng và tỷ ở lớp 5
Chia 2 trường hợp \(\overline{ab}=2x\overline{cd}\) hoặc \(\overline{cd}=2x\overline{ab}\)
Bạn tự làm nốt nhé

\(\left(-x-\dfrac{1}{2}y\right)\left(-x+\dfrac{1}{2}y\right)\\ =\left[\left(-x\right)-\dfrac{1}{2}y\right]\left[\left(-x\right)+\dfrac{1}{2}y\right]\\ =\left(-x\right)^2-\left(\dfrac{1}{2}y\right)^2\\ =x^2-\dfrac{y^2}{4}\)


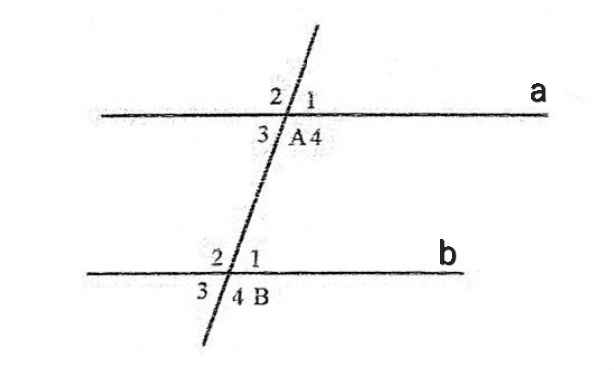
Ta có:
∠A₃ = ∠B₁ (gt)
Mà ∠A₃ và ∠B₁ là hai góc so le trong
⇒ a // b
⇒ ∠A₂ = ∠B₂ (đồng vị)
Do ∠A₃ + ∠A₄ = 180⁰ (kề bù)
Mà ∠A₃ = ∠B₁ (gt)
⇒ ∠B₁ + ∠A₄ = 180⁰

\(M=\dfrac{202}{7\cdot1010}+\dfrac{202}{10\cdot1313}+\dfrac{202}{13\cdot1616}+...+\dfrac{202}{91\cdot9494}\\ =\dfrac{202}{7\cdot10\cdot101}+\dfrac{202}{10\cdot13\cdot101}+\dfrac{202}{13\cdot16\cdot101}+...+\dfrac{202}{91\cdot94\cdot101}\\ =\dfrac{202}{101}\cdot\left(\dfrac{1}{7\cdot10}+\dfrac{1}{10\cdot13}+\dfrac{1}{13\cdot16}+...+\dfrac{1}{91\cdot94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+...+\dfrac{3}{91\cdot94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{91}-\dfrac{1}{94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{1}{7}-\dfrac{1}{94}\right)\\ =\dfrac{2}{3}\cdot\dfrac{87}{658}\\ =\dfrac{29}{329}\)
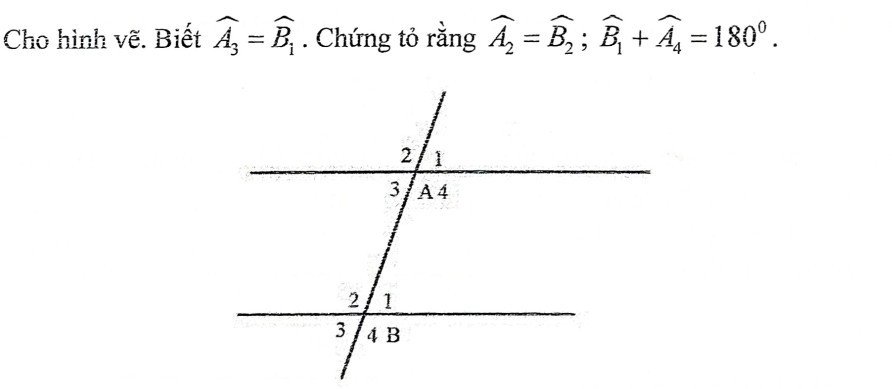 mng giúp e vs ạ
mng giúp e vs ạ
Áp dụng BĐT trị tuyệt đối, ta có:
\(\left|x-9\right|+\left|2-x\right|\ge\left|x-9+2-x\right|=\left|7\right|=7\)
Dấu "=" xảy ra khi: \(\left(x-9\right)\left(2-x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-9\ge0\\2-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-9\le0\\2-x\le0\end{matrix}\right.\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge9\\x\le2\end{matrix}\right.\left(\text{vô lí}\right)\\\left\{{}\begin{matrix}x\le9\\x\ge2\end{matrix}\right.\end{matrix}\right.\\ \Rightarrow2\le x\le9\)
\(\left|x-9\right|+\left|2-x\right|=7\)
Ta có : \(\left|x-9\right|+\left|2-x\right|\ge\left|x-9+2-x\right|=7\)
Nên \(x=0\) là nghiệm phương trình đã cho.