\(f\left(x\right)=ax^2+bx+c\)

Mà: \(f\left(0\right)=2\) thay `x=0` ta có:

\(\Rightarrow f\left(0\right)=a\cdot0^2+b\cdot0+c=2\Rightarrow c=2\) 

       \(f\left(1\right)=7\) thay `x=1` ta có:

\(\Rightarrow f\left(1\right)=a\cdot1^2+b\cdot1+c=7\Rightarrow a+b+c=7\Rightarrow a+b=5\) (vì `c = 2`) 

\(\Rightarrow a=5-b\) (*) 

      \(f\left(-2\right)=-14\) 

\(\Rightarrow f\left(-2\right)=a\cdot\left(-2\right)^2+b\cdot-2+c=-14\)

\(\Rightarrow4a-2b+c=-14\)

\(\Rightarrow4a-2b=-16\) (vì `c=2`) 

\(\Rightarrow2a-b=-8\) (**) 

Thay (*) vào (**) ta có:

\(2\cdot\left(5-b\right)-b=-8\)

\(\Rightarrow10-2b-b=-8\)

\(\Rightarrow-3b=-18\)

\(\Rightarrow b=6\)

\(\Rightarrow a=5-6=-1\)

Vậy: ... 

Ta có: \(\dfrac{y+z+1}{x}=\dfrac{x+z+2}{y}=\dfrac{x+y-3}{z}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{y+z+1}{x}=\dfrac{x+z+2}{y}=\dfrac{x+y-3}{z}=\dfrac{y+z+1+x+z+2+x+y-3}{x+y+z}\)

\(=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\) 

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y+z}=2\\\dfrac{y+z+1}{x}=2\\\dfrac{x+z+2}{y}=2\\\dfrac{x+y-3}{z}=2\end{matrix}\right.\) 

Ta có: \(\dfrac{1}{x+y+z}=2\Rightarrow x+y+z=\dfrac{1}{2}\) 

\(\dfrac{y+z+1}{x}=2\Rightarrow y+z+1=2x\Rightarrow\left(x+y+z\right)+1=3x\)

\(\Rightarrow\dfrac{1}{2}+1=3x\)

\(\Rightarrow3x=\dfrac{3}{2}\Rightarrow x=\dfrac{1}{2}\)  

\(x+y+z=\dfrac{1}{2}\Rightarrow y+z=0\Rightarrow y=-z\)  

\(\dfrac{x+z+2}{y}=2\Rightarrow\dfrac{\dfrac{1}{2}+z+2}{-z}=2\Rightarrow\dfrac{5}{2}+z=-2z\)

\(\Rightarrow3z=-\dfrac{5}{2}\Rightarrow z=-\dfrac{5}{6}\)

\(\Rightarrow y=-\left(-\dfrac{5}{6}\right)=\dfrac{5}{6}\)

Vậy: \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{5}{6};-\dfrac{5}{6}\right)\)

Ta có:

`4x-5y-6xy+7=0`

`⇒(4x-6xy)-5y+7=0`

`⇒2x(2-3y)-5y+7=0`

`⇒6x(2-3y)-15y+21=0` 

`⇒6x(2-3y)+21-15y=0` 

`⇒6x(2-3y)+(10-15y)+11=0`

`⇒-6x(3y-2)-(15y-10)+11=0`

`⇒-6x(3y-2)-5(3y-2)=-11`

`⇒(3y-2)(6x+5)=11` 

Mà `x,y∈Z` 

Ta có bảng: 

Vậy: ... 

\(\dfrac{4^6\cdot9^5+6^9\cdot120}{8^4\cdot3^{12}-6^{11}}\)

\(=\dfrac{\left(2^2\right)^6\cdot\left(3^2\right)^5+\left(3^9\cdot2^9\right)\cdot\left(2^3\cdot3\cdot5\right)}{\left(2^3\right)^4\cdot3^{12}-2^{11}\cdot3^{11}}\)

\(=\dfrac{2^{12}\cdot3^{10}+3^{10}\cdot2^{12}\cdot5}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}\)

\(=\dfrac{2^{12}\cdot3^{10}\cdot\left(1+5\right)}{2^{11}\cdot3^{11}\cdot\left(2\cdot3-1\right)}\)

\(=\dfrac{2\cdot6}{3\cdot5}\)

\(=\dfrac{4}{5}\)

Gọi a (tờ), b (tờ), c (tờ) lần lượt là số tờ tiền polime ứng với loại 20000 đồng, 50000 đồng và 100000 đồng (a, b, c ∈ ℕ*)

Do tổng số tờ tiền là 24 tờ nên ta có:

a + b + c = 24

Do trị giá của mỗi loại tiền là như nhau nên:

20000a = 50000b = 100000c

2a = 5b = 10c

⇒ a/(1/2) = b/(1/5) = c/(1/10)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/(1/2) = b/(1/5) = c/(1/10) = (a + b + c)/(1/2 + 1/5 + 1/10) = 24/(4/5) = 30

2a = 30 ⇒ a = 30 : 2 = 15 (nhận)

5b = 30 ⇒ b = 30 : 5 = 6 (nhận)

10c = 30 ⇒ c = 30 : 10 = 3 (nhận)

Vậy số tờ tiền ứng với loại 20000 đồng; 50000 đồng; 10000 đồng lần lượt là: 15 tờ, 6 tờ; 3 tờ

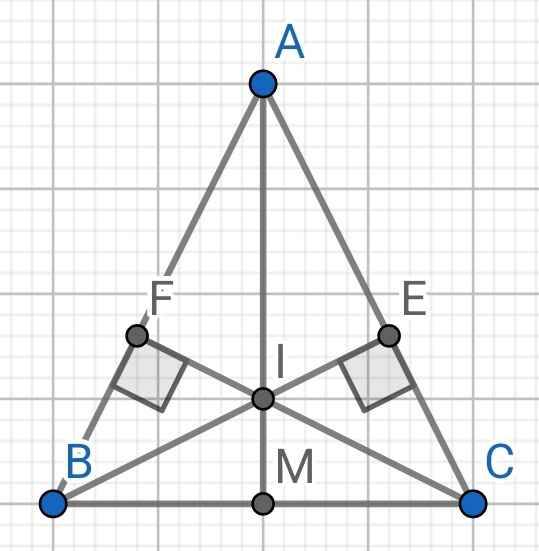
Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆ABE và ∆ACF có:

AB = AC (cmt)

∠A chung

⇒ ∆ABE = ∆ACF (cạnh huyền - góc nhọn)

b) Do ∆ABE = ∆ACF (cmt)

⇒ AE = AF (hai cạnh tương ứng)

Ta có:

BF = AB - AF

CE = AC - AE

Mà AB = AC (cmt)

AF = AE (cmt)

⇒ BF = CE

Do ∆ABE = ∆ACF (cmt)

⇒ ∠ABE = ∠ACF (hai góc tương ứng)

⇒ ∠FBI = ∠ECI

Xét hai tam giác vuông: ∆FBI và ∆ECI có:

BF = CE (cmt)

∠FBI = ∠ECI (cmt)

⇒ ∆FBI = ∆ECI (cạnh góc vuông - góc nhọn kề)

⇒ BI = IC (hai cạnh tương ứng)

⇒ ∆BIC cân tại I

c) ∆FBI vuông tại F

⇒ BI là cạnh huyền nên là cạnh lớn nhất

⇒ BI > FI

Mà BI = IC (cmt)

⇒ IC > FI

d) Do ∆ABC cân tại A (gt)

M là trung điểm của BC (gt)

⇒ AM là đường trung tuyến của ∆ABC

⇒ AM cũng là đường cao của ∆ABC

Mà I là giao điểm của hai đường cao BE và CF

⇒ A, I, M thẳng hàng