Ta có:

$\frac{1}{2^2}<\frac{1}{1.2};\frac{1}{3^2}<\frac{1}{2.3};...;\frac{1}{{100}^2}<\frac{1}{99.100}$

Đặt:

$A=1+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{{100}^2}$

$\to A<1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}=1+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=2-\frac{1}{100}<2$

$\to 1+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{{100}^2}<2$

$\to$đpcm

nhớ tick cho mik nha

cách 2 : 

Đặt 1+1/2^2+1/3^2+...+1/100^2=A

Có A<1+1/1.2+1/2.3+1/3.4+....+1/99.100

=>A<1+1-1/2+1/2-1/3+1/3-1/4+....+1/99-1/100

=>A<1+1-1/100

=>A<2-1/100<2

nhớ tickkk

a: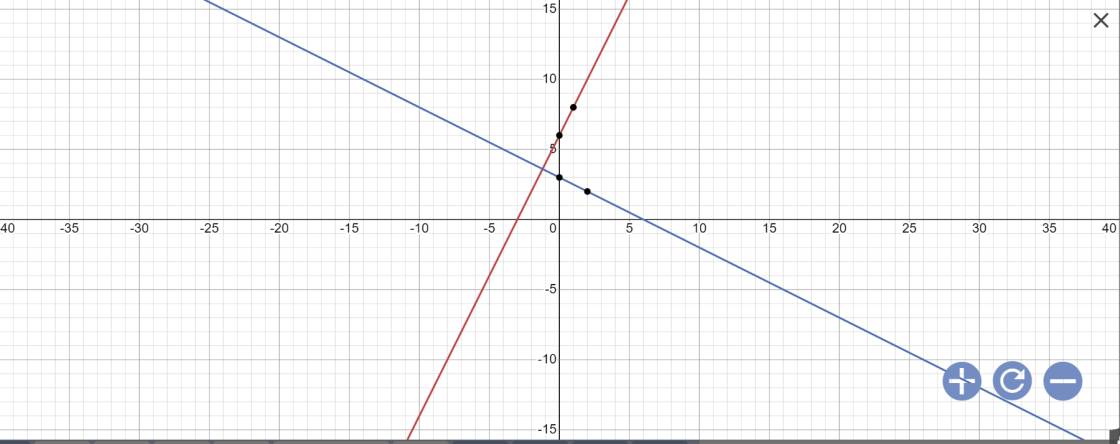 

b: Phương trình hoành độ giao điểm là:

\(2x+6=-\dfrac{1}{2}x+3\)

=>\(\dfrac{5}{2}x=-3\)

=>\(x=-3:\dfrac{5}{2}=-\dfrac{6}{5}\)=-1,2

Thay x=-1,2 vào y=2x+6, ta được:

\(y=2\cdot\left(-1,2\right)+6=3,6\)

vậy: C(-1,2;3,6)

c: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\2x+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=0\end{matrix}\right.\)

vậy: A(-3;0); B(6;0); C(-1,2;3,6)

\(AB=\sqrt{\left(6+3\right)^2+\left(0-0\right)^2}=9\)

\(AC=\sqrt{\left(-1,2+3\right)^2+\left(3,6-0\right)^2}=\dfrac{9\sqrt{5}}{5}\)

\(BC=\sqrt{\left(-1,2-6\right)^2+\left(3,6-0\right)^2}=\dfrac{18\sqrt{5}}{5}\)

Vì \(AC^2+BC^2=AB^2\)

nên ΔABC vuông tại C

=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{9}{\sqrt{5}}\cdot\dfrac{18}{\sqrt{5}}=\dfrac{81}{5}\)

d: (d2): y=-1/2x+3

=>\(-\dfrac{1}{2}x-y+3=0\)

\(d\left(M;\left(d2\right)\right)=\dfrac{\left|0\cdot\left(-\dfrac{1}{2}\right)+\left(-3\right)\cdot\left(-1\right)+3\right|}{\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(-1\right)^2}}=6:\dfrac{\sqrt{5}}{2}=\dfrac{12}{\sqrt{5}}\)

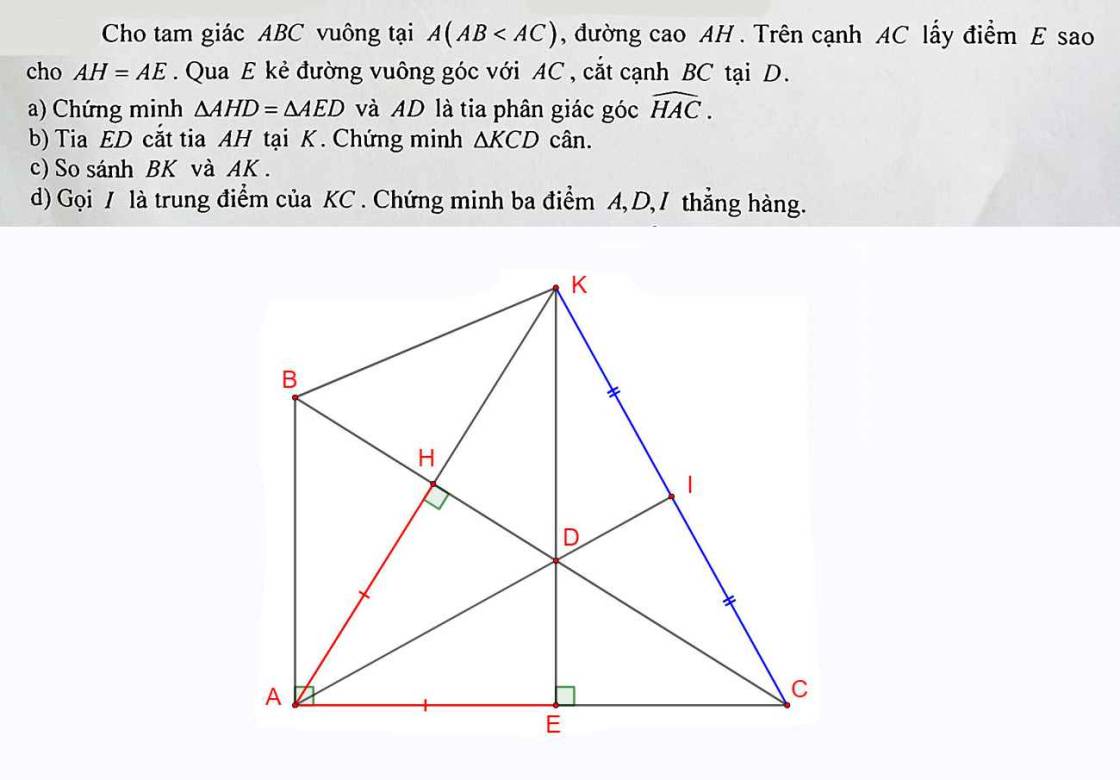
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có

AD chung

AH=AE

Do đó: ΔAHD=ΔAED

=>\(\widehat{HAD}=\widehat{EAD}\)

=>AD là phân giác của góc HAC

b: Ta có: ΔAHD=ΔAED

=>DH=DE

Xét ΔDHK vuông tại H và ΔDEC vuông tại E có

DH=DE

\(\widehat{HDK}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDHK=ΔDEC
=>DK=DC

=>ΔDKC cân tại D

d: Ta có: ΔDHK=ΔDEC

=>HK=EC

Ta có: AH+HK=AK

AE+EC=AC

mà AH=AE và HK=EC

nên AK=AC

=>A nằm trên đường trung trực của KC(1)

Ta có: DK=DC

=>D nằm trên đường trung trực củaKC(2)

Ta có: IC=IK

=>I nằm trên đường trung trực của KC(3)

Từ (1),(2),(3) suy ra A,D,I thẳng hàng

\(\dfrac{2}{3^2}< \dfrac{2}{1\cdot3}=1-\dfrac{1}{3}\)

\(\dfrac{2}{5^2}< \dfrac{2}{3\cdot5}=\dfrac{1}{3}-\dfrac{1}{5}\)

...

\(\dfrac{2}{99^2}< \dfrac{2}{97\cdot99}=\dfrac{1}{97}-\dfrac{1}{99}\)

Do đó: \(A=\dfrac{2}{3^2}+\dfrac{2}{5^2}+...+\dfrac{2}{99^2}< 1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

=>\(A< 1-\dfrac{1}{99}=\dfrac{98}{99}\)

\(\dfrac{2}{3^2}>\dfrac{2}{3\cdot5}=\dfrac{1}{3}-\dfrac{1}{5}\)

\(\dfrac{2}{5^2}>\dfrac{2}{5\cdot7}=\dfrac{1}{5}-\dfrac{1}{7}\)

...

\(\dfrac{2}{99^2}>\dfrac{2}{99\cdot101}=\dfrac{1}{99}-\dfrac{1}{101}\)

Do đó: \(A=\dfrac{2}{3^2}+\dfrac{2}{5^2}+...+\dfrac{2}{99^2}>\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
=>\(A>\dfrac{1}{3}-\dfrac{1}{101}=\dfrac{98}{303}\)

=>\(\dfrac{98}{303}< A< \dfrac{98}{99}\)

Mình cảm ơn bạn Phước Thịnh nhé!

Dịch chuyển dấu phẩy của A sang trái một hàng thì được số B nên B=10A

Dịch chuyển dấu phẩy của A sang phải một hàng thì được số C nên C=0,1A

A+B+C=135,975

=>A+10A+0,1A=135,975

=>11,1A=135,975

=>A=12,25

                                 Giải:

Vì dịch dấu phẩy số A sang trái một hàng ta được số B nên số B bằng:

                     1 : 10 = \(\dfrac{1}{10}\) (số A)

Vì dịch dấu phẩy của số A sang phải một hàng ta được số C nên số C bằng:

                     1 x 10 = \(\dfrac{10}{1}\) (số A)

135,975 ứng với phân số là:

               1 + \(\dfrac{1}{10}\) + \(\dfrac{10}{1}\) = \(\dfrac{111}{10}\) (số A)

Số A là: 135,975 : \(\dfrac{111}{10}\) =  12,25

Đs:..

A = \(\dfrac{n+1}{3n-1}\) (n \(\in\) Z)

n \(\in\) Z để phân số làm sao em?

đề thiếu rồi em

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{NBA}\) là góc tạo bởi tiếp tuyến BA và dây cung BN

\(\widehat{BMN}\) là góc nội tiếp chắn cung BN

Do đó: \(\widehat{NBA}=\widehat{BMN}\)

mà \(\widehat{BMN}=\widehat{KAN}\)(hai góc so le trong, BM//AC)

nên \(\widehat{KAN}=\widehat{KBA}\)

Xét ΔKAN và ΔKBA có

\(\widehat{KAN}=\widehat{KBA}\)

\(\widehat{AKN}\) chung

Do đó: ΔKAN~ΔKBA

=>\(\dfrac{KA}{KB}=\dfrac{KN}{KA}\)

=>\(KA^2=KB\cdot KN\)(1)

c: Xét (O) có

\(\widehat{KCN}\) là góc tạo bởi tiếp tuyến CK và dây cung CN

\(\widehat{CBN}\) là góc nội tiếp chắn cung CN

Do đó: \(\widehat{KCN}=\widehat{CBN}=\widehat{KBC}\)

Xét ΔKCN và ΔKBC có

\(\widehat{KCN}=\widehat{KBC}\)

\(\widehat{CKN}\) chung

Do đó: ΔKCN~ΔKBC

=>\(\dfrac{KC}{KB}=\dfrac{KN}{KC}\)

=>\(KC^2=KB\cdot KN\left(2\right)\)

Từ (1) và (2) suy ra KA=KC

=>K là trung điểm của AC

ΔOCA vuông tại C

=>\(CO^2+CA^2=OA^2\)

=>\(CA^2=\left(3R\right)^2-R^2=8R^2\)

=>\(CA=R\cdot2\sqrt{2}\)

=>\(KA=R\sqrt{2}\)

d: Gọi giao điểm của MN và OE là I, giao điểm của BC và OA là H

Xét (O) có

EM,EN là các tiếp tuyến

Do đó: EM=EN

=>E nằm trên đường trung trực của MN(3)

Ta có: OM=ON

=>O nằm trên đường trung trực của MN(4)

Từ (3) và (4) suy ra OE là đường trung trực của MN

=>OE\(\perp\)MN tại I và I là trung điểm của MN

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(5)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(6)

Từ (5),(6) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại H

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\left(7\right)\)

Xét ΔONE vuông tại N có NI là đường cao

nên \(OI\cdot OE=ON^2\left(8\right)\)

Từ (7) và (8) suy ra \(OH\cdot OA=OI\cdot OE\)

=>\(\dfrac{OH}{OI}=\dfrac{OE}{OA}\)

Xét ΔOHE và ΔOIA có

\(\dfrac{OH}{OI}=\dfrac{OE}{OA}\)

\(\widehat{HOE}\) chung

Do đó: ΔOHE~ΔOIA

=>\(\widehat{OHE}=\widehat{OIA}=90^0\)

=>\(\widehat{OHE}=\widehat{OHB}=90^0\)

=>H,B,E thẳng hàng

mà B,H,C thẳng hàng

nên E,B,C thẳng hàng

Số số hạng là \(\dfrac{401-1}{1}+1=401\left(số\right)\)

Tổng của dãy số là \(\left(401+1\right)\cdot\dfrac{401}{2}=401\cdot201=80601\)

\(\dfrac{2}{5}\times\dfrac{9}{5}+\dfrac{1}{3}:\dfrac{2}{6}\\ =\dfrac{18}{25}+\dfrac{1}{3}\times\dfrac{6}{2}\\ =\dfrac{18}{25}+1\\ =\dfrac{18}{25}+\dfrac{25}{25}\\ =\dfrac{43}{25}\)