Bài 3: (2 điểm) Tìm một số có hai chữ số biết răng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 6 đơn vị, nếu đổi hai chữ số cho nhau ta được một số mới mà tổng của số mới và số cũ là 132.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.
a.
Áp dụng đẳng thức: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow\left(\dfrac{1}{3}\right)^2+cos^2\alpha=1\)
\(\Rightarrow cos^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Rightarrow cos\alpha=\dfrac{2\sqrt{2}}{3}\) (do \(\alpha\) nhọn nên \(cos\alpha>0\))
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{\sqrt{2}}{4}\)
b.
\(P=sin^21^0+sin^289^0+sin^22^0+sin^288^0+...+sin^244^0+sin^246^0+sin^245^0+sin^290^0\)
\(=sin^21^0+sin^2\left(90^0-1^0\right)+sin^22^0+sin^2\left(90^0-2^0\right)+...+sin^244^0+sin^2\left(90^0-44^0\right)+\left(\dfrac{\sqrt{2}}{2}\right)^2+1^2\)
\(=sin^21^0+cos^21^0+sin^22^0+cos^22^0+...+sin^244^0+cos^244^0+\dfrac{3}{2}\)
\(=1+1+...+1+\dfrac{3}{2}\) (có 44 số 1)
\(=44+\dfrac{3}{2}=\dfrac{91}{2}\)
c.
\(\dfrac{1-tan\alpha}{1+tan\alpha}=\dfrac{1-\dfrac{sin\alpha}{cos\alpha}}{1+\dfrac{sin\alpha}{cos\alpha}}=\dfrac{\dfrac{cos\alpha-sin\alpha}{cos\alpha}}{\dfrac{cos\alpha+sin\alpha}{cos\alpha}}=\dfrac{cos\alpha-sin\alpha}{cos\alpha+sin\alpha}\)

ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
- Với \(-\dfrac{1}{4}\le x\le0\Rightarrow\left\{{}\begin{matrix}x^4< \dfrac{1}{4^4}< 1\\\sqrt[4]{4x+1}\ge0\Rightarrow4\sqrt[4]{4x+1}+1\ge1\end{matrix}\right.\)
\(\Rightarrow x^4< 4\sqrt[4]{4x+1}+1\) nên pt vô nghiệm
- Với \(x>0\):
Đặt \(\sqrt[4]{4x+1}=a>0\Rightarrow4x+1=a^4\)
Ta được hệ:
\(\left\{{}\begin{matrix}x^4=4a+1\\a^4=4x+1\end{matrix}\right.\)
Trừ vế cho vế:
\(\Rightarrow x^4-a^4=4\left(a-x\right)\)
\(\Leftrightarrow\left(x-a\right)\left(x+a\right)\left(x^2+a^2\right)+4\left(x-a\right)=0\)
\(\Leftrightarrow\left(x-a\right)\left[\left(x+a\right)\left(x^2+a^2\right)+4\right]=0\)
\(\Leftrightarrow x=a\) (do \(\left(x+a\right)\left(x^2+a^2\right)+4>0\) với \(a;x>0\))
\(\Leftrightarrow x=\sqrt[4]{4x+1}\)
\(\Leftrightarrow x^4=4x+1\)
\(\Leftrightarrow x^4-4x-1=0\)
\(\Leftrightarrow\left(x^4+2x^2+1\right)-\left(2x^2+4x+2\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)^2-2\left(x+1\right)^2=0\)
\(\Leftrightarrow x^2+1=\sqrt{2}\left(x+1\right)\) (do \(x>0\) nên chỉ có TH này xảy ra khi khai căn)
\(\Leftrightarrow x^2-\sqrt{2}x+1-\sqrt{2}=0\)
Pt bậc 2 bình thường, em có thể tính delta và giải theo công thức nghiệm

Gọi số lớn là x, số nhỏ là y
Do hiệu 2 số là 272 nên ta có pt:
\(x-y=272\) (1)
Do số lớn chia số nhỏ được 4 dư 56 nên:
\(x=4y+56\Leftrightarrow x-4y=56\) (2)
Từ (1) và (2) ta được hệ:
\(\left\{{}\begin{matrix}x-y=272\\x-4y=56\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=344\\y=72\end{matrix}\right.\)
Đặt \(x\) là số nhỏ
\(\Rightarrow\) Số lớn \(=4x+56\)
Khi đó, ta có: \(4x+56-x=272\) và ta tìm được \(x=72\)
Nên số lớn là \(344\)
Vậy hai số đó là \(72\) và \(344\)

ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
\(\Leftrightarrow\left(x+1\right)^3+\left(x+1\right)=\left(3x+1+1\right)\sqrt{3x+1}\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{3x+1}=b\ge0\end{matrix}\right.\)
Pt trở thành:
\(a^3+a=\left(b^2+1\right)b\)
\(\Leftrightarrow a^3-b^3+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2+1\right)=0\)
\(\Leftrightarrow a-b=0\) (do \(a^2+ab+b^2+1=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}+1>0\))
\(\Leftrightarrow\sqrt{3x+1}=x+1\)
\(\Leftrightarrow3x+1=x^2+2x+1\)
\(\Rightarrow x=\left\{0;1\right\}\)

Với mọi x;y dương ta có:
\(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge x^2+y^2+2xy\)
\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow\sqrt{x^2+y^2}\ge\dfrac{x+y}{\sqrt{2}}\)
Áp dụng:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\ge\dfrac{a+b}{\sqrt{2}}+\dfrac{b+c}{\sqrt{2}}+\dfrac{c+a}{\sqrt{2}}=\sqrt{2}\left(a+b+c\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
- Với BĐT bên phải: \(\sqrt{3}\left(a+b+c\right)>\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\)
Áp dụng BĐT Bunhiacopxki:
\(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{3\left(a^2+b^2+b^2+c^2+c^2+a^2\right)}\)
\(\Leftrightarrow\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\le\sqrt{6\left(a^2+b^2+c^2\right)}\)
Nên ta chỉ cần chứng minh:
\(\sqrt{3}\left(a+b+c\right)>\sqrt{6\left(a^2+b^2+c^2\right)}\)
\(\Leftrightarrow\left(a+b+c\right)^2>2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\)
Thật vậy, do a, b, c là 3 cạnh của 1 tam giác nên theo BĐT tam giác:
\(\left\{{}\begin{matrix}a< b+c\\b< c+a\\c< a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2< a\left(b+c\right)\\b^2< b\left(c+a\right)\\c^2< c\left(a+b\right)\end{matrix}\right.\)
Cộng vế:
\(a^2+b^2+c^2< 2ab+2bc+2ca\) (đpcm)

Sửa lại Gia đình bà Vân gồm 4 người lớn và 3 trẻ em thanh toán \(110000\) đồng thành \(1100000\) đồng
Gọi giá buffet của người lớn và trẻ em lần lượt là \(x;y\left(x;y>0\right)\)
Tổng số tiền ông Khanh : \(5x+5y=1500000\)
\(\Rightarrow x+y=300000\left(2\right)\)
Tổng số tiền nhà bà Vân : \(4x+3y=1100000\left(2\right)\)
\(\left(1\right);\left(2\right)\) ta có HPT :
\(\left\{{}\begin{matrix}x+y=300000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+4y=1200000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=300000\\y=100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=200000\\y=100000\end{matrix}\right.\)
Vậy giá buffet của người lớn và trẻ em lần lượt là \(200000\left(đồng\right);100000\left(đồng\right)\)
Em kiểm tra lại đề, rất có thể ở dữ liệu nhà bà Vân em ghi thiếu 1 số 0 ở con số 110 000, lẽ ra phải là 1 100 000 mới hợp lý

Câu 2:
a: \(cosa=0\)
=>\(a=90^0\)
b: \(tana=\dfrac{\sqrt{3}}{3}\)
=>\(a=arctan\left(\dfrac{\sqrt{3}}{3}\right)=30^0\)
c: \(cota-sin90^0=0\)
=>\(cota=sin90^0=1\)
=>\(a=45^0\)
d: \(tana=\dfrac{sina}{cota}\)
=>\(\dfrac{sina}{cosa}=\dfrac{sina}{cota}\)
=>\(cota=cosa\)
=>\(cosa\left(\dfrac{1}{sina}-1\right)=0\)
=>\(\left[{}\begin{matrix}cosa=0\\sina=1\end{matrix}\right.\Leftrightarrow a=90^0\)

\(\left(a+1\right)^2-2a-2\)
\(=a^2+2a+1-2a-2=a^2-1< =0\)(Do \(a^2< =1\))
=>\(\left(a+1\right)^2< =2a+2\)
Vì a2 ≤ 1 ⇒ a2 + 1 ≤ 1 + 1 = 2
⇒ a2 + 1 + 2a ≤ 2 + 2a ⇒ (a + 1)2 ≤ 2(đpcm)

Gọi chiều rộng ban đầu là x(m)
(Điều kiện: \(0< x< \dfrac{35}{2}\))
Chiều dài ban đầu là 35-x(m)
Chiều dài sau khi giảm đi 5m là 35-x-5=30-x(m)
Diện tích nhỏ hơn ban đầu là 75m2 nên ta có:
x(35-x)-x(30-x)=75
=>\(35x-x^2-30x+x^2=75\)
=>5x=75
=>x=15(nhận)
Vậy: Chiều rộng ban đầu là 15m
Chiều dài ban đầu là 35-15=20m
Diện tích ban đầu là \(15\cdot20=300\left(m^2\right)\)
Gọi chiều dài và chiều rộng của khu vườn hình chữ nhật lúc đầu lần lượt là `x` và `y (m)`
Điều kiện: `0 <x,y < 35`
Do Khu vườn hình chữ nhật có tổng chiều dài và chiều rộng là 35m
`=> x+y = 35 (1)`
Do nếu giảm chiều dài 5m và giữ nguyên chiều rộng thì diện tích vườn nhỏ hơn lúc đầu là `75m^2` nên
`xy - (x-5)y = 75`
`=> xy -xy +5y = 75`
`=> 5y = 75
`=> y = 15`
Khi đó: `x = 35 - 15 = 20` (Thỏa mãn)
Diện tích khu vườn ban đầu là:
`xy = 20 . 15 = 300 (m^2)`
Vậy diện tích khu vườn ban đầu là `300m^2`

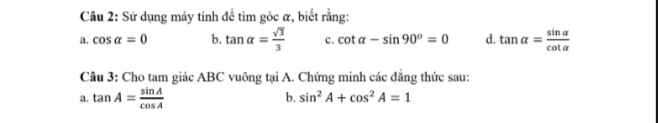
93
Gọi số cần tìm có dạng là \(\overline{ab}\)
Chữ số hàng chục lớn hơn chữ số hàng đơn vị là 6 đơn vị nên a-b=6
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới và số cũ là 132 nên \(\overline{ab}+\overline{ba}=132\)
=>10a+b+10b+a=132
=>11a+11b=132
=>a+b=12
mà a-b=6
nên \(a=\dfrac{12+6}{2}=9;b=12-9=3\)
Vậy: Số cần tìm là 93