Cho hình chóp S.ABCD, gọi O là giao điểm AC và BD. Lấy M,N lần lượt thuộc cạnh SA, SC.
a) Tìm (BMN) giao SO
b) Tìm (BMN) giao SD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(u_0=\dfrac{1}{2.0^2-3}=-\dfrac{1}{3};u_1=\dfrac{1}{2.1^2-3}=-1\)
Ta có \(u_{n+1}=\dfrac{1}{2\left(n+1\right)^2-3}< \dfrac{1}{2n^2-3}=u_n\) với \(n\ge2\)
Khi đó \(\left\{u_n\right\}\) là dãy giảm với \(n\ge2\). Do đó \(u_n\le u_2=\dfrac{1}{2.2^2-3}=\dfrac{1}{5}\) hay \(\left\{u_n\right\}\) bị chặn trên bởi \(\dfrac{1}{5}\).
Mặt khác, với \(n\ge2\) thì \(u_n>0\). Do đó \(\left\{u_n\right\}\) bị chặn dưới bởi \(-1\).

Nếu \(n\) chẵn thì đpcm trở thành \(\dfrac{3n+1}{4n-1}\le\dfrac{3n+4}{4n-1}\) \(\Leftrightarrow3n+1\le3n+4\) \(\Leftrightarrow1\le4\), luôn đúng.
Nếu \(n\) lẻ thì đpcm thành \(\dfrac{3n-1}{4n+1}\le\dfrac{3n+4}{4n-1}\)
\(\Leftrightarrow\left(3n-1\right)\left(4n-1\right)\le\left(4n+1\right)\left(3n+4\right)\)
\(\Leftrightarrow12n^2-3n-4n+1\le12n^2+16n+3n+4\)
\(\Leftrightarrow26n+3\ge0\) (luôn đúng)
Vậy với mọi \(n\inℕ^∗\) thì \(\dfrac{3n+\left(-1\right)^n}{4n-\left(-1\right)^n}\le\dfrac{3n+4}{4n-1}\)

Câu 3:
\(u_1=\dfrac{2\cdot1+1}{1+2}=\dfrac{3}{3}=1\)
\(u_4=\dfrac{2\cdot4+1}{4+2}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(u_5=\dfrac{2\cdot5+1}{5+2}=\dfrac{11}{7}\)
Câu 2:
\(u_n=u_1+\left(n-1\right)\cdot d\)
=>\(-3\left(n-1\right)+4=-41\)
=>-3(n-1)=-45
=>n-1=15
=>n=16
Câu 1:
Tổng của 50 số hạng đầu là 5150
=>\(\dfrac{n\cdot\left[2\cdot u_1+\left(n-1\right)\cdot d\right]}{2}=5150\)
=>\(\dfrac{50\left(2\cdot5+\left(50-1\right)\cdot d\right)}{2}=5150\)
=>\(25\left(10+49d\right)=5150\)
=>49d+10=206
=>49d=196
=>d=4
\(u_{10}=u_1+9d=5+9\cdot4=5+36=41\)

Câu 1:
-2;x;-18;y là cấp số nhân
=>\(\left\{{}\begin{matrix}x^2=\left(-2\right)\cdot\left(-18\right)\\\left(-18\right)^2=x\cdot y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=36\\xy=324\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=\dfrac{324}{6}=54\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=\dfrac{324}{-6}=-54\end{matrix}\right.\end{matrix}\right.\)
=>Chọn C
Câu 2:
\(u_4=u_2\cdot q^2\)
=>\(4q^2=9\)
=>\(q^2=\dfrac{9}{4}=\left(\dfrac{3}{2}\right)^2\)
=>\(\left[{}\begin{matrix}q=\dfrac{3}{2}\\q=-\dfrac{3}{2}\end{matrix}\right.\)
TH1: q=3/2
\(u_2=q\cdot u_1\)
=>\(u_1=\dfrac{u_2}{q}=4:\dfrac{3}{2}=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\)
\(u_5=u_1\cdot q^4=\dfrac{8}{3}\cdot\left(\dfrac{3}{2}\right)^4=\dfrac{8}{3}\cdot\dfrac{81}{16}=\dfrac{27}{2}\)
\(u_8=u_1\cdot q^7=\dfrac{8}{3}\cdot\left(\dfrac{3}{2}\right)^7=\dfrac{2^3}{3}\cdot\dfrac{3^7}{2^7}=\dfrac{3^6}{2^4}=\dfrac{729}{16}\)
TH2: q=-3/2
\(u_1=\dfrac{u_2}{q}=4:\dfrac{-3}{2}=4\cdot\dfrac{-2}{3}=-\dfrac{8}{3}\)
\(u_5=u_1\cdot q^4=-\dfrac{8}{3}\cdot\left(-\dfrac{3}{2}\right)^4=-\dfrac{8}{3}\cdot\dfrac{81}{16}=\dfrac{-27}{2}\)
\(u_8=u_1\cdot q^7=\dfrac{-8}{3}\cdot\left(-\dfrac{3}{2}\right)^7=\dfrac{-2^3}{3}\cdot\dfrac{\left(-3\right)^7}{2^7}=\dfrac{2^3}{3}\cdot\dfrac{3^7}{2^7}=\dfrac{3^4}{2^4}=\dfrac{81}{16}\)
Câu 3:
\(\left\{{}\begin{matrix}u_1+u_5=51\\u_2+u_6=102\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1\cdot q^4=51\\u_1\cdot q+u_1\cdot q^5=102\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q^4=51\\q\left(u_1+u_1\cdot q^4\right)=102\end{matrix}\right.\Leftrightarrow q=2\)
\(u_1+u_5=51\)
=>\(u_1\left(1+q^4\right)=51\)
=>\(u_1=\dfrac{51}{2^4+1}=\dfrac{51}{17}=3\)
\(u_4=u_1\cdot q^3=3\cdot2^3=24\)
\(u_{12}=u_1\cdot q^{11}=3\cdot2^{11}=6144\)

Câu 1: \(u_4=u_1+3k\)
=>\(3k=\dfrac{3}{8}-3=\dfrac{3}{8}-\dfrac{24}{8}=-\dfrac{21}{8}\)
=>\(k=-\dfrac{7}{8}\)
\(u_7=u_1+6k=3+6\cdot\dfrac{-7}{8}=3-\dfrac{42}{8}=\dfrac{24-42}{8}=-\dfrac{18}{8}=-\dfrac{9}{4}\)
Câu 2:
\(\dfrac{u_5}{u_8}=8\)
=>\(\dfrac{u_1\cdot q^4}{u_1\cdot q^7}=8\)
=>\(\dfrac{1}{q^3}=8\)
=>\(q=\dfrac{1}{2}\)
\(u_{12}=u_1\cdot q^{11}=12\cdot\left(\dfrac{1}{2}\right)^{11}=\dfrac{12}{2^{11}}=\dfrac{3}{2^9}\)
Câu 3:
Tổng của 5 số hạng đầu là:
\(S_5=\dfrac{u_1\cdot\left(1-q^5\right)}{1-q}=\dfrac{2\cdot\left(1-4^5\right)}{1-4}=682\)
=>Chọn D

Câu 25:
\(0< \alpha< \dfrac{\Omega}{2}\)
=>\(0< sin\alpha< 1;0< cos\alpha< 1\)
\(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\)
\(=\dfrac{1+sin\alpha+1-sin\alpha}{cos\alpha}=\dfrac{2}{cos\alpha}\)
Câu 28:
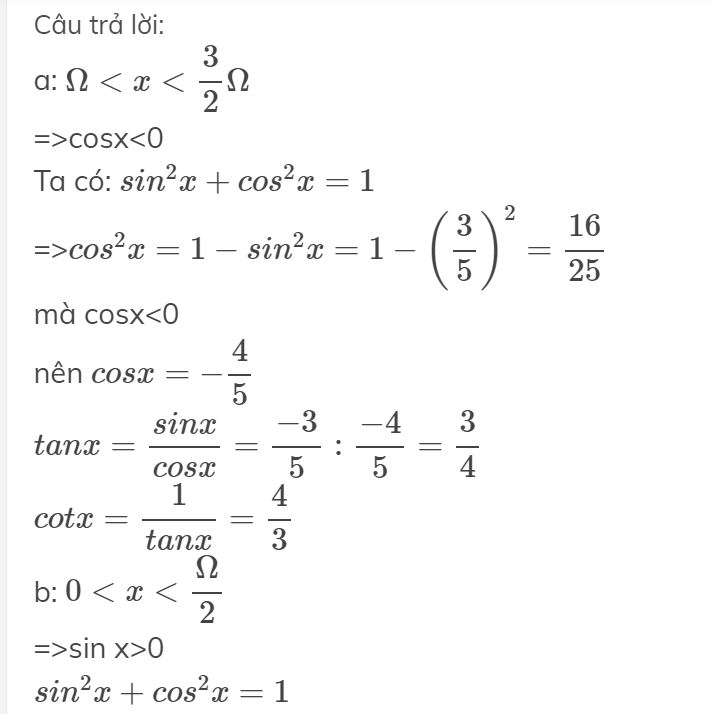
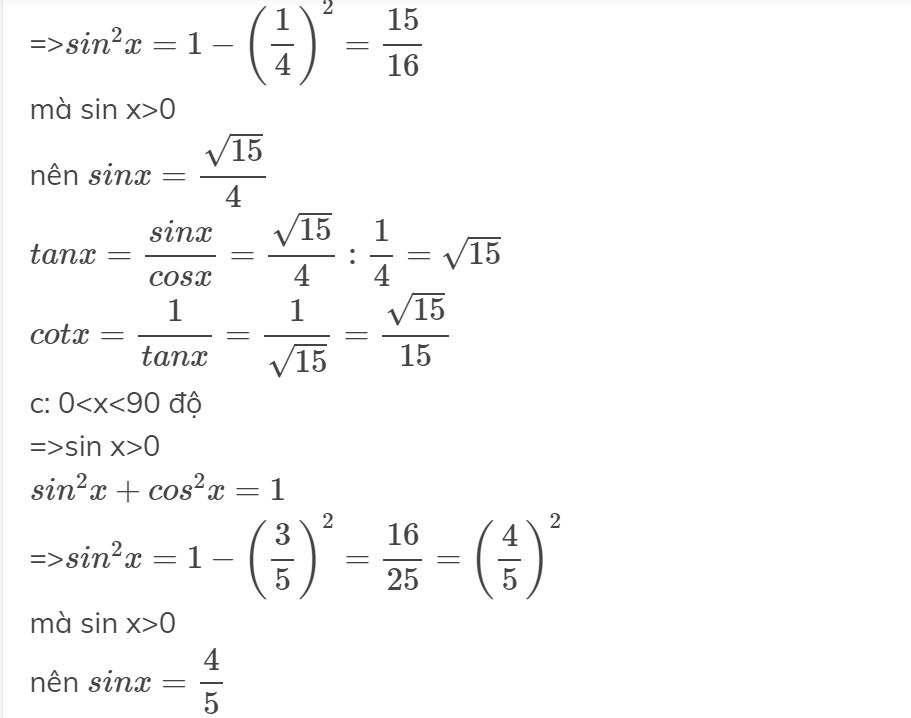


a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)

\(A=2\cdot cos\left(\dfrac{\Omega}{2}+x\right)+sin\left(5\Omega-x\right)+sin\left(\dfrac{3\Omega}{2}+x\right)+cos\left(\dfrac{\Omega}{2}+x\right)\)
\(=3\cdot cos\left(\dfrac{\Omega}{2}+x\right)+sin\left(\Omega-x\right)+sin\left(\dfrac{\Omega}{2}+\Omega+x\right)\)
\(=-3\cdot sinx+sinx+cos\left(\Omega+x\right)\)
\(=-2\cdot sinx-cosx\)
\(B=sin\left(\Omega+x\right)-cos\left(\dfrac{\Omega}{2}+x\right)+cot\left(2\Omega-x\right)+tan\left(\dfrac{2\Omega}{2}+x\right)\)
\(=-sinx+sinx+cot\left(-x\right)+tan\left(x\right)\)
\(=tanx-cotx=tanx-\dfrac{1}{tanx}=\dfrac{tan^2x-1}{tanx}\)
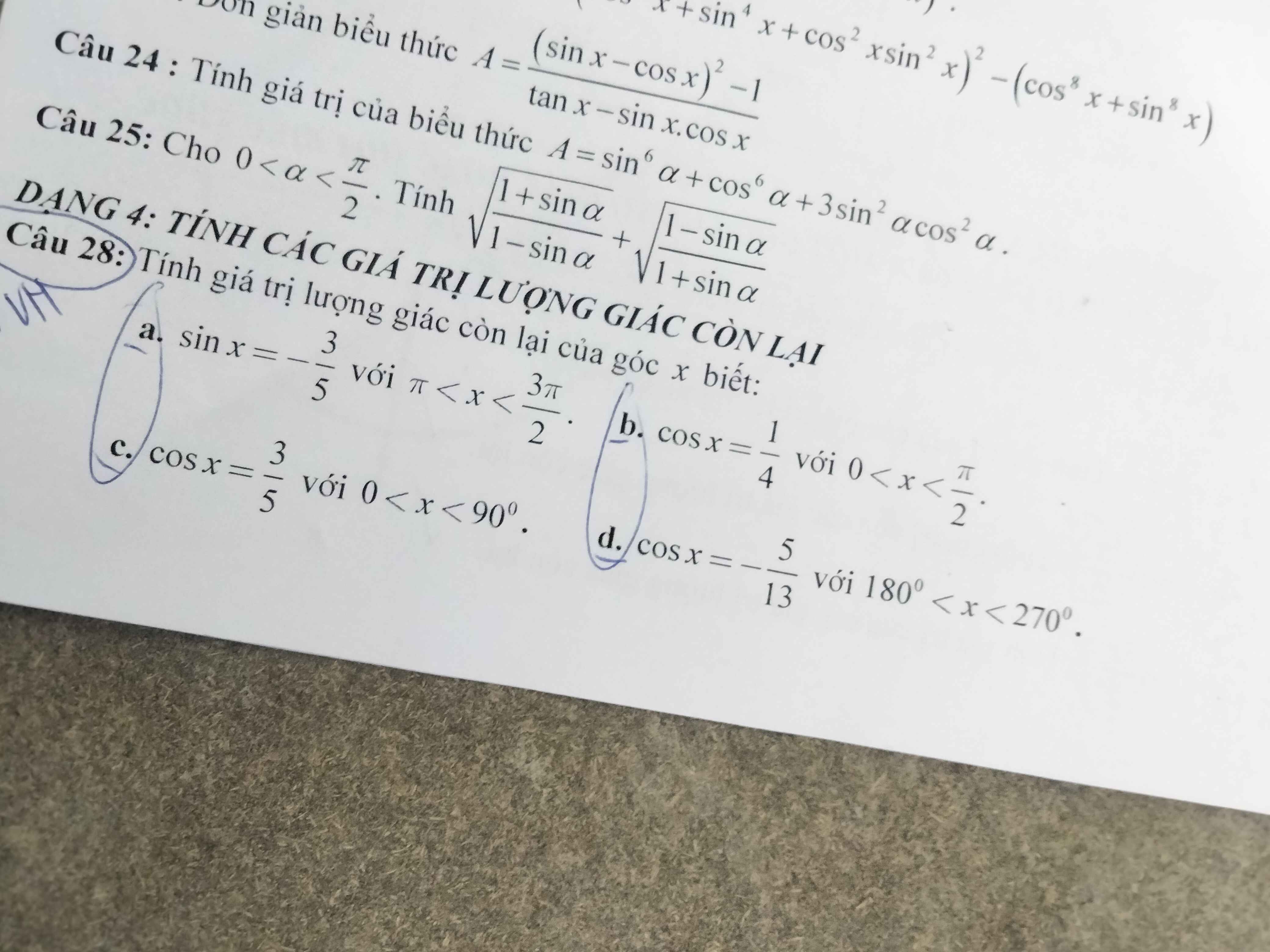
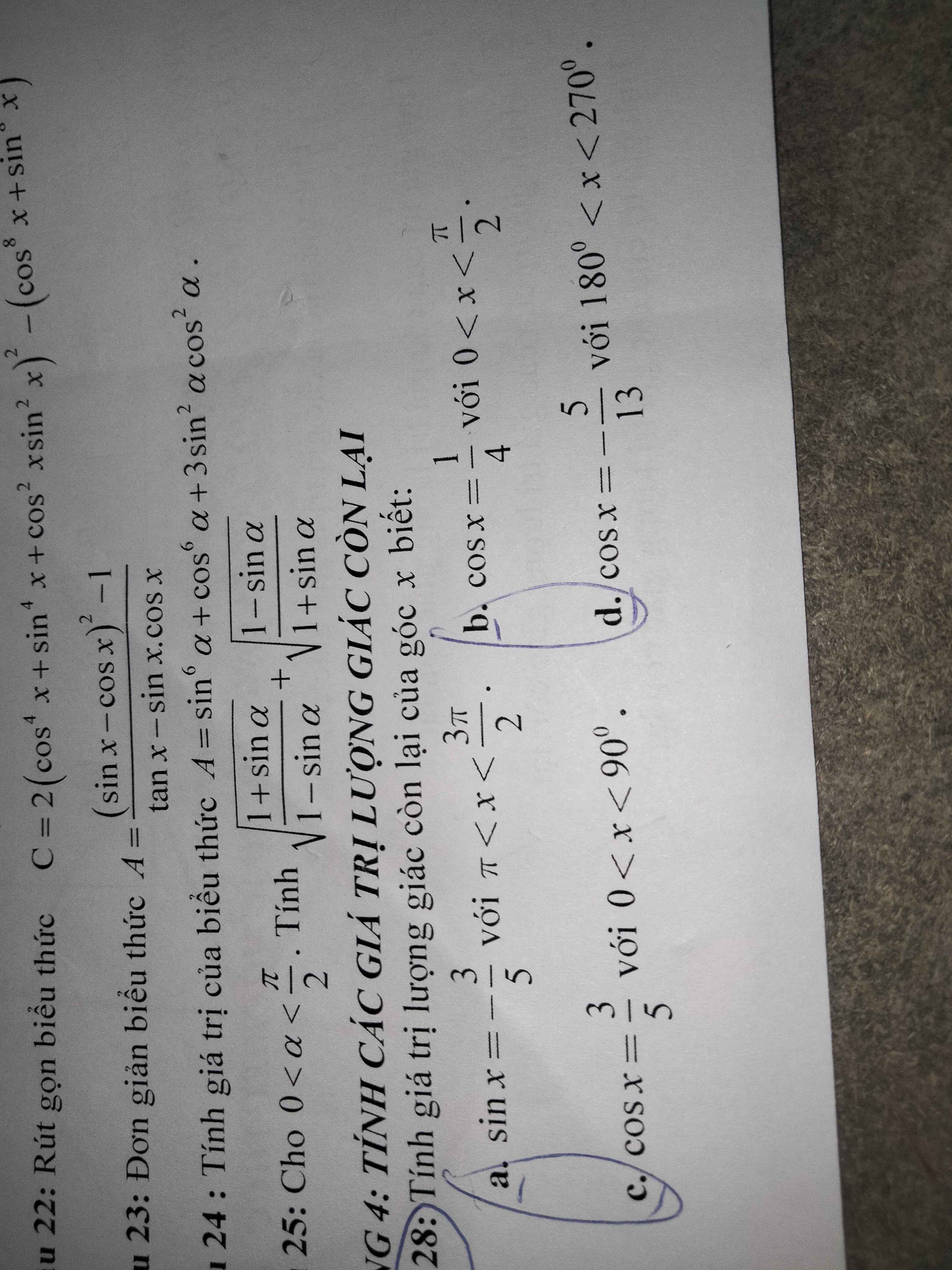
a) Trong mặt phẳng (SAC), gọi I là giao điểm của AO và MN. Khi đó vì \(MN\subset\left(BMN\right)\) nên I chính là giao điểm của (BMN) và SO.
b) Ta có \(I\in SO\subset\left(SBD\right)\) nên \(I\in\left(SBD\right)\). Trong mặt phẳng (SBD), gọi K là giao điểm của BI và SD. Khi đó vì \(K\in BI\subset\left(BMN\right)\) nên K chính là giao điểm của (BMN) và SD.
a: Trong mp(SAC), gọi K là giao điểm của MN với SO
mà MN\(\in\left(BMN\right)\)
nên \(K=SO\cap\left(BMN\right)\)
b: Vì K là giao của MN và SO
mà \(MN\in\left(BMN\right);SO\in\left(SBD\right)\)
nên \(K\in\left(BMN\right)\cap\left(SBD\right)\)
mà \(B\in\left(BMN\right)\cap\left(SBD\right)\)
nên \(\left(BMN\right)\cap\left(SBD\right)=BK\)
Gọi E là giao điểm của BK với SD
=>K là giao điểm của SD với (BMN)