hay
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`P=3x^2-3x^4+1/2x^5+0,75`
`=1/2x^5-3x^4+3x^2+0,75`
Bậc của B chính là bậc của hạng tử có bậc cao nhất là `1/2x^5` có bậc 5
`=>P` có bậc 5`

là những từ loại để dùng để chỉ số lượng thứ tự của sự vật nào đó ák bn.

Bài này kết quả -11 đúng không cả nhà ơi
= 2(-1) - 5.1 + 4.-1 -3 = -11
Khi x=-1 thì \(P\left(-1\right)=2\cdot\left(-1\right)^3-5\cdot\left(-1\right)^2+4\cdot\left(-1\right)-3\)
\(=2\cdot\left(-1\right)-5\cdot1-4-3\)
=-2-5-4-3
=-7-3-4
=-14

**Giới thiệu nghề làm than tại Quảng Ninh** Quảng Ninh – mảnh đất giàu tài nguyên khoáng sản, từ lâu đã gắn liền với hình ảnh những người thợ mỏ cần cù, chịu khó trong nghề làm than. Đây không chỉ là một nghề đặc trưng, mà còn là biểu tượng văn hóa và niềm tự hào của vùng đất mỏ. Với lịch sử hàng trăm năm phát triển, nghề làm than đã góp phần to lớn vào sự nghiệp công nghiệp hóa đất nước. Những người thợ mỏ Quảng Ninh – với chiếc mũ bảo hộ, đôi bàn tay chai sạn và tinh thần “Kỷ luật và Đồng tâm” – đã trở thành hình ảnh đẹp, thể hiện nghị lực phi thường và tình yêu lao động. Ngày nay, ngành công nghiệp khai thác than tại Quảng Ninh không ngừng đổi mới, áp dụng công nghệ hiện đại, góp phần bảo vệ môi trường và phát triển bền vững. Nghề làm than không chỉ mang lại giá trị kinh tế lớn, mà còn là linh hồn của Quảng Ninh – vùng đất "rồng bay lên" giữa thời kỳ hội nhập.

Ta có: \(\left(3x-\dfrac{1}{6}\right)^2>=0\forall x\)
\(\left|2y-6\right|>=0\forall y\)
Do đó: \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|>=0\forall x,y\)
mà \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|< =0\)
nên \(\left\{{}\begin{matrix}3x-\dfrac{1}{6}=0\\2y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{1}{6}\\2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{18}\\y=3\end{matrix}\right.\)
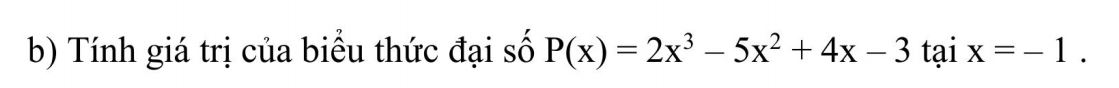

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!
uhhhhhh:<