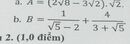\(ĐK:x\ge-2\)

\(\sqrt{2x+5}-\sqrt{x+2}=\frac{x+3}{5}\)

\(\Leftrightarrow\frac{x+3}{\sqrt{2x+5}+\sqrt{x+2}}=\frac{x+3}{5}\)

\(\Leftrightarrow\left(x+3\right)\left(\frac{1}{\sqrt{2x+5}+\sqrt{x+2}}-\frac{1}{5}\right)=0\)

\(\Leftrightarrow\frac{1}{\sqrt{2x+5}+\sqrt{x+2}}-\frac{1}{5}=0\)(Do \(x\ge-2\)nên \(x+3\ge1>0\))

Xét phương trình \(\frac{1}{\sqrt{2x+5}+\sqrt{x+2}}-\frac{1}{5}=0\Leftrightarrow\sqrt{2x+5}+\sqrt{x+2}=5\)

\(\Leftrightarrow\left(\sqrt{2x+5}-3\right)+\left(\sqrt{x+2}-2\right)=0\)

\(\Leftrightarrow\frac{2x-4}{\sqrt{2x+5}+3}+\frac{x-2}{\sqrt{x+2}+2}=0\)

\(\Leftrightarrow\left(x-2\right)\left(\frac{2}{\sqrt{2x+5}+3}+\frac{1}{\sqrt{x+2}+2}\right)=0\)

Dễ thấy \(\frac{2}{\sqrt{2x+5}+3}+\frac{1}{\sqrt{x+2}+2}>0\forall x\ge-2\)nên x - 2 = 0 hay x = 2 (t/m)

Vậy phương trình có 1 nghiệm duy nhất là 2

Đk: \(4x^2+5x+1\ge0\)

\(\sqrt{4x^2+5x+1}+3=2\sqrt{x^2-x+1}+9x\)

<=> \(\sqrt{4x^2+5x+1}-\sqrt{4x^2-4x+4}=9x-3\)

Đặt \(\sqrt{4x^2+5x+1}=a\left(a\ge0\right)\)

\(\sqrt{4x^2-4x+4}=b\left(b>0\right)\)

=> \(a^2-b^2=4x^2+5x+1-4x^2+4x-4=9x-3\)

mà a - b = 9x - 3

=> a² - b² = a - b

<=> (a + b)(a - b) - (a - b) = 0

<=> (a - b)(a + b- 1) = 0

<=> \(\orbr{\begin{cases}a=b\\a+b=1\end{cases}}\)

<=> \(\orbr{\begin{cases}\sqrt{4x^2+5x+1}=\sqrt{4x^2-4x+4}\\\sqrt{4x^2+5x+1}=1-\sqrt{4x^2-4x+4}\end{cases}}\)

(còn lại tự giải: bình phương lên là đc)

\(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\frac{x+3}{2}\)

\(\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}=\frac{x+3}{2}\)

\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}=\frac{x+3}{2}\)

\(\Leftrightarrow\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|=\frac{x+3}{2}\)

TH1 \(\sqrt{x-1}>1\Rightarrow PT\Leftrightarrow\sqrt{x-1}+1+\sqrt{x-1}-1=\frac{x+3}{2}\)

\(\Leftrightarrow2\sqrt{x-1}=\frac{x+3}{2}\Leftrightarrow16\left(x-1\right)=\left(x+3\right)^2\Leftrightarrow x^2-10x+25=0\Leftrightarrow x=5\) thỏa mãn

TH2 \(\sqrt{x-1}\le1\Rightarrow PT\Leftrightarrow\sqrt{x-1}+1-\sqrt{x-1}+1=\frac{x+3}{2}\)

\(\Leftrightarrow2=\frac{x+3}{2}\Leftrightarrow x=1\)thỏa mãn

Trục căn thức thôi bạn

\(B=\frac{1}{\sqrt{5}-2}+\frac{4}{3+\sqrt{5}}=\frac{\sqrt{5}+2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}+\frac{4\left(3-\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\)

\(=\frac{\sqrt{5}+2}{5-4}+\frac{4\left(3-\sqrt{5}\right)}{9-5}\)

\(=\frac{\sqrt{5}+2}{1}+\frac{4\left(3-\sqrt{5}\right)}{4}\)

\(=\sqrt{5}+2+3-\sqrt{5}=5\)