Tìm hai số tự nhiên biết tổng của chúng bằng 221 và ước chung lớn nhất của chúng bằng 13
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vận tốc lúc đi so với vận tốc lúc về bằng: 10/12= 5/6
Tổng số phần bằng nhau: 5+6=11 (phần)
Đổi 3h40p=11/3h
Thời gian về bằng:
11/3 : 11 x 5 = 5/3(h)
Quãng đường AB dài:
5/3 x 12= 20(km)
Đ.số: 20km

\(\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{5}\right)=\dfrac{30}{70}+\left(-\dfrac{175}{70}\right)+\left(-\dfrac{42}{70}\right)=-\dfrac{187}{70}\)
\(\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{5}\right)=\dfrac{3}{7}-\dfrac{5}{2}-\dfrac{3}{5}\)
\(=\dfrac{30}{70}-\dfrac{175}{70}-\dfrac{42}{70}=-\dfrac{187}{70}\)

a) \(BCNN\left(3;8\right)=24\)
\(\Rightarrow x=24\) thỏa đề bài
b) \(BCNN\left(12;18;30\right)=180\)
\(\Rightarrow x=180\) thỏa đề bài

a) Ta có 111 chia hết cho 37 mà các số dạng aaa khi nào cũng chia hết cho 111 ⇒ Các số có dạng aaa luôn chia hết cho 37 (ĐPCM)
b) Ta có ab-ba=a.10+b-b.10-a=9.a-9.b=9.(a-b)
Vì 9 chia hết cho 9 ⇒ 9.(a-b) chia hết cho 9 ⇒ ab-ba bao giờ cũng chia hết cho 9 (ĐPCM)
c) Ta có 2 trường hợp n có hạng 2k hoặc 2k+1
+) Nếu n= 2k thì n+6 chia hết cho 2 ⇒ (n+3)(n+6) chia hết cho 2
+) Nếu n= 2k+1 thì n+3 chia hết cho 2 ⇒ (n+3)(n+6) chia hết cho 2
⇒ (n+3)(n+6) chia hết cho 2 với mọi n là số tự nhiên
a) \(\overline{aaa}=100a+10a+a=111a\)
mà \(111=37.3⋮37\)
\(\Rightarrow\overline{aaa}⋮37\left(dpcm\right)\)
b) \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b=9\left(a-b\right)⋮9\left(a\ge b\right)\)
\(\Rightarrow dpcm\)

\(\left[\left(2,18-1,38\right).1,25\right]:\left[\left(17,9-15,65\right):1,125\right]:\left(-0,4\right)\)
\(=\left[0,18.1,25\right]:\left[2,25:1,125\right]:\left(-0,4\right)\)
\(=\left[0,225\right]:\left[2\right]:\left(-0,4\right)\)
\(=\left[0,225\right]:\left[2\right]:\left(-0,4\right)=-0,045\)
[ (2,18 - 1,38).1,25]: [(17,9 - 15,65): 1,125]:(-0,4)
= [0,8.1,25]: [(2,25): 1,125]:(-0,4)
= 1:[ (2,25): 1,125]:(-0,4)
= 1:(2):(-0,4)
= 0,5: -(0,4)
= - \(\dfrac{5}{4}\)


55.25.125.5 = 5^5 . 5^2 . 5^3 . 5^1 = 5^(5 + 2 + 3 + 1) = 5^11

132.21= 44.3.21= 44. 63= 63.44
Vậy: 63.44 = 132.21

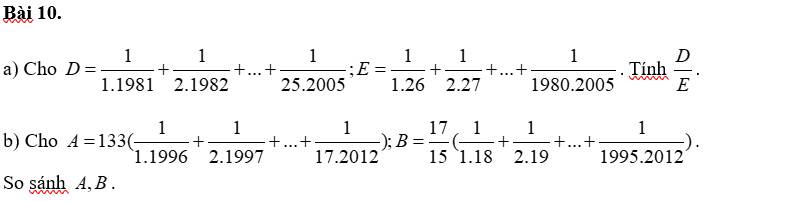 Help me PLS
Help me PLS
\(\left\{{}\begin{matrix}a+b=221\\UCLN\left(a;b\right)=13\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=13m\\b=13n\\\left(m;n\right)=1\end{matrix}\right.\)
\(\Rightarrow13m+13n=221\)
\(\Rightarrow13\left(m+n\right)=221\)
\(\Rightarrow m+n=17\)
- Với \(\left\{{}\begin{matrix}m=16\\n=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=208\\b=13\end{matrix}\right.\)
- Với \(\left\{{}\begin{matrix}m=14\\n=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=182\\b=39\end{matrix}\right.\)
- Với \(\left\{{}\begin{matrix}m=12\\n=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=156\\b=65\end{matrix}\right.\)
- Với \(\left\{{}\begin{matrix}m=10\\n=7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=130\\b=91\end{matrix}\right.\)
- Với \(\left\{{}\begin{matrix}m=6\\n=11\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=78\\b=143\end{matrix}\right.\)
\(\Rightarrow\left(a;b\right)\in\left\{\left(108;13\right);\left(182;39\right);\left(156:65\right);\left(130;91\right);\left(78;143\right)\right\}\)