Bình đọc một quyển truyện trong 3 ngày. Ngày đầu đọc đc 1/5 số trang và 16 trang. Ngày thứ hai Bình đọc đc 3/10 số trang còn lại và 20 trang. Ngày thứ ba đọc đc 3/4 số trang còn lại và 37 trang cuối cùng. Hỏi quyển truyện đó có bao nhiêu trang?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#040911`
\(5^x\cdot5^{x+1}\cdot5^{x+2}=5^9?\)
\(\Rightarrow5^{x+x+1+x+2}=5^9\\ \Rightarrow5^{3x+3}=5^9\\ \Rightarrow3x+3=9\\ \Rightarrow3x=6\\ \Rightarrow x=6\div3\\ \Rightarrow x=2\)
Vậy, `x=2.`
5x . 5x + 1 . 5x + 2 = 59
5x + x + 1 + x + 2 = 59
x + x + 1 + x + 2 = 9
3x + 3 = 9
3x = 9 - 3
x = 6 : 3
x = 2
Vậy x = 2

\((x - 3).(2y + 1) = 7\)
Ý của bạn là chỉ yc tìm mỗi vế của biến x ạ?
\(\left(x-3\right)\cdot\left(2y+1\right)\in\text{Ư}\left(7\right)=\left\{1;7;-1;-7\right\}\)
`\Rightarrow \text {TH1:} x - 3 = 1`
`\Rightarrow x = 1 + 3`
`\Rightarrow x = 4`
`\text {TH2:} x - 3 = 7`
`\Rightarrow x = 7 + 3`
`\Rightarrow x = 10`
`\text {TH3:} x - 3 = -1`
`\Rightarrow x = -1 + 3`
`\Rightarrow x = 2`
`\text {TH4:} x - 3 = -7`
`\Rightarrow x = -7 + 3`
`\Rightarrow x = -4`
Vậy, `x \in {-4; 4; 2; 10}`
ta có
trường hợp 1:(x-3)=7
x-3=7
x=7+3
x=10
x-3=7
x=7+3
x=10
trường hợp 2:(x-3)=1
x-3=1
x=1+3
x=4

Lời giải:
a.
$(5x-6)(1999^2+2.1999+1)=4.10^3$
$(5x-6)(1999+1)^2=(4.10^3)^2=4000^2$
$(5x-6).2000^2=4000^2$
$5x-6=\frac{4000^2}{2000^2}=2^2=4$
$5x=10$
$x=10:5=2$
b.
$(23545-7^5)x:[(8^4-4.10^3)^2-2478]=1$
$6738.x:6738=1$
$x=1$

1)5x +12 = 22
5x = 22 - 12
5x = 10
x = 2
2)45 : x + 100 =105
45 : x = 105 - 100
45 :x = 5
x = 45 : 5
x= 9
77-2.x =17
2.x = 77 - 17
2.x = 60
x = 60 :2
x= 30
88-18.x = 70
18.x = 88 - 70
18 .x = 18
x = 1

\(\Rightarrow x\in BC\left(24,36\right)\)
Ta có: \(24=2^3.3\\ 36=2^2.3^2\)
\(\Rightarrow x\in BCNN\left(24,36\right)=2^3.3^2=72\\ \Rightarrow B\left(72\right)=\left\{0;72;144;216;288;360;...\right\}\)
mà \(250\le x\le350\)
\(\Rightarrow x=288\).
Vậy \(x=288.\)

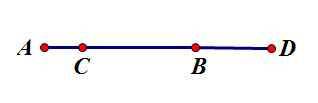
\(a.\) \(CB=AB-AC=4-1=3\) \(cm\)
\(b.\) \(CD=CB+BD=3+2=5\) \(cm\)

\(A=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).\left(1-\dfrac{1}{5}\right)...\left(1-\dfrac{1}{2003}\right).\left(1-\dfrac{1}{2004}\right).\)
\(\Rightarrow A=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.\dfrac{4}{5}....\dfrac{2002}{2003}.\dfrac{2003}{2004}\)
\(\Rightarrow A=\dfrac{1}{2004}\)
\(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)...\left(1-\dfrac{1}{2004}\right)\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}...\dfrac{2003}{2004}\\ =\dfrac{1}{2004}\)
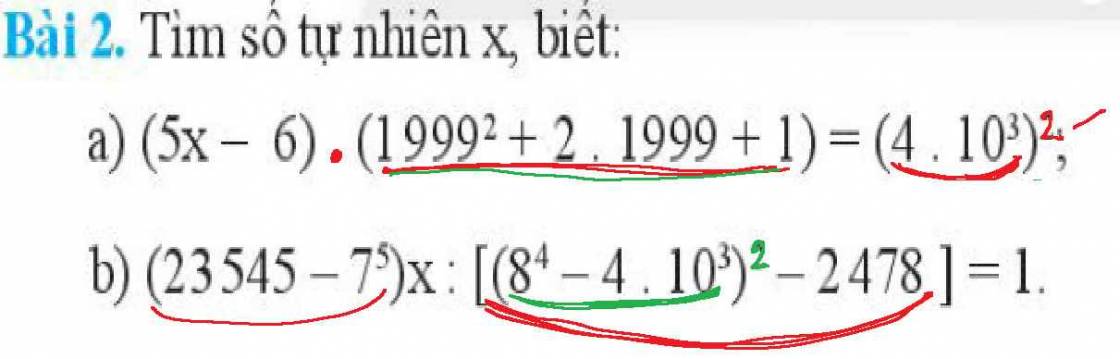
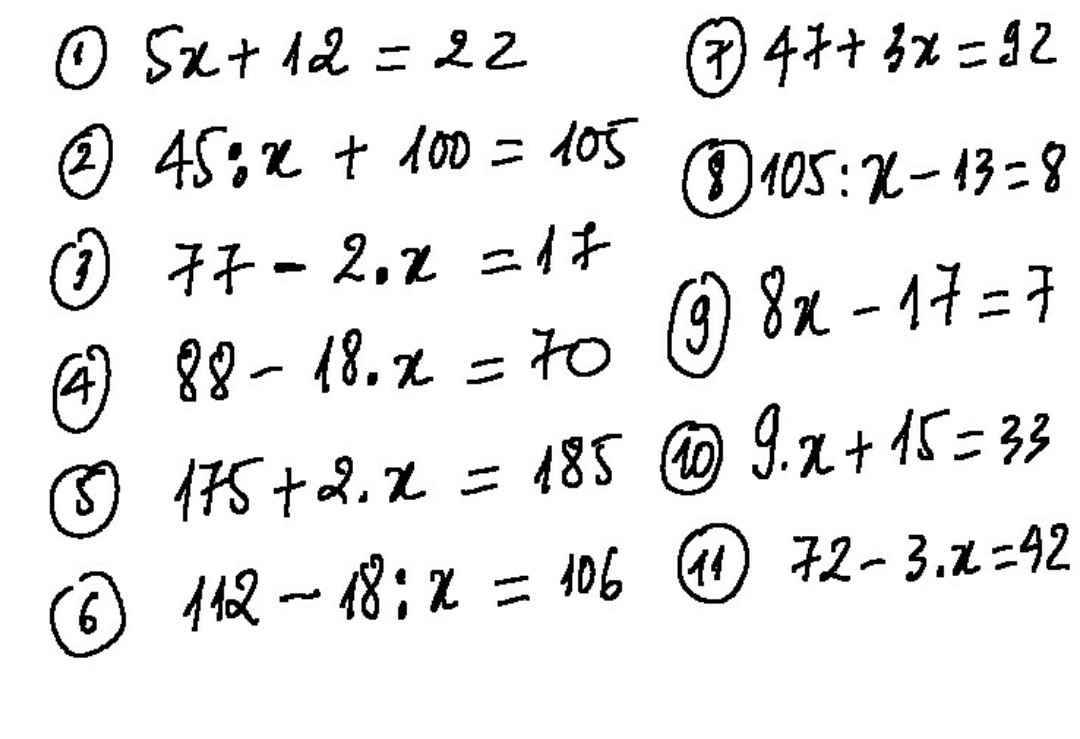
37 trang cuối ứng với: 1 - \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\) (số trang còn lại sau ngày thứ hai)
Số trang còn lại sau ngày thứ hai là:
37 : \(\dfrac{1}{4}\) = 148 (trang)
Nếu ngày thứ hai không đọc thêm 20 trang thì số trang còn lại sau ngày thứ hai là:
148 + 20 = 168 (trang)
168 trang ứng với : 1 - \(\dfrac{3}{10}\) = \(\dfrac{7}{10}\) (số trang còn lại sau ngày thứ nhất)
Số trang còn lại sau ngày thứ nhất là:
168 : \(\dfrac{7}{10}\) = 240 (trang)
Nếu ngày thứ nhất không đọc thêm 16 trang thì số trang còn lạ sau ngày thứ nhất là:
240 + 16 = 256 (trang)
256 ứng với phân số là: 1 - \(\dfrac{1}{5}\) = \(\dfrac{4}{5}\) (số trang)
Quyển truyện dày số trang là: 256 : \(\dfrac{4}{5}\) = 320 (trang)
Kết luận: Quyển truyện dày 320 trang .