K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
30 tháng 1 2018
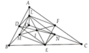
Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I

29 tháng 10 2016
Xét tg OAC có
FA=FC
NO=NC
=> NF là đường trung bình => NF//OA và NF=OA/2 (1)
Xét tg OAB chứng minh tương tự => MD//)A và MD=OA/2 (2)
Từ (1) và (2) => NF//=MD => MDFN là hình bình hành => DN cắt FM tại trung điểm mỗi đường (*)
Chứng minh tương tự cũng có EDLF là hình bình hành => DN cắt EL tại trung điểm mỗi đường (**)
Từ (*) và (**) => EL; FM; DN đều cắt nhau tại trung điểm mỗi đường nên chúng đồng quy
kết bạn với tui nha[nếu rảnh]
Xét ΔDAO có
D,M lần lượt là trung điểm của BA,BO
=>DM là đường trung bình của ΔDAO
=>DM//AO và \(DM=\frac{AO}{2}\)
Xét ΔCAO có
F,N lần lượt là trung điểm của CA,CO
=>FN là đường trung bình của ΔCAO
=>FN//AO và \(FN=\frac{AO}{2}\)
Ta có: DM//AO
FN//AO
Do đó: DM//FN
Ta có: \(DM=\frac{AO}{2}\)
\(FN=\frac{AO}{2}\)
Do đó: DM=FN
Xét ΔABO có
D,L lần lượt là trung điểm của AB,AO
=>DL là đường trung bình của ΔABO
=>DL//BO và \(DL=\frac{BO}{2}\)
Xét ΔBOC có
E,N lần lượt là trung điểm của CB,CO
=>EN là đường trung bình của ΔBOC
=>EN//BO và \(EN=\frac{BO}{2}\)
Ta có: DL//BO
EN//BO
Do đó: DL//EN
Ta có: \(DL=\frac{BO}{2}\)
\(EN=\frac{BO}{2}\)
Do đó: DL=EN
Xét tứ giác DLNE có
DL//NE
DL=NE
Do đó: DLNE là hình bình hành
=>DN cắt LE tại trung điểm của mỗi đường(1)
Xét tứ giác DFNM có
DM//FN
DM=FN
Do đó: DFNM là hình bình hành
=>DN cắt FM tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra DN,LE,FM đồng quy