Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E
Gọi AH và AK lần lượt là 2 đường cao của \(\Delta ADE\)và \(\Delta ABC\)
Xét tứ giác BCDE có \(\widehat{BEC}=\widehat{BDC}=90^o\)nên tứ giác BCDE nội tiếp
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)( cùng bù với \(\widehat{BED}\))
\(\Rightarrow\Delta ADE\approx\Delta ABC\left(g.g\right)\) ( nếu chưa học tứ giác nội tiếp thì có thể xét các tam giác đồng dạng để c.m nha )
\(\Rightarrow\frac{AD}{AB}=\frac{DE}{BC}=\frac{AH}{AK}\) ( vì tỉ số đồng dạng bằng tỉ số đường cao )
a) Ta có : \(\frac{S_{ADE}}{S_{ABC}}=\frac{\frac{DE.AH}{2}}{\frac{BC.AK}{2}}=\frac{AD}{AB}.\frac{AH}{AK}=\left(\frac{AD}{AB}\right)^2\)
Mà \(\cos A=\frac{AD}{AB}\Rightarrow\cos^2=\left(\frac{AD}{AB}\right)^2\)\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\cos^2A\)
\(\Rightarrow S_{ADE}=S_{ABC}.\cos^2A\)
b) \(S_{BCDE}=S_{ABC}-S_{ADE}=S_{ABC}.\left(1-\cos^2A\right)=S_{ABC}.\sin^2A\)( vì \(\cos^2A+\sin^2A=1\))

a) Xét tứ giác AEHF có
\(\widehat{HEA}+\widehat{HFA}=180^0\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Xét tam giác AEF và tam giác ABC có:
A chung
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(=cosA\right)\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2A=1-sin^2A\)
\(1-\sin^2A=\cos^2A=\dfrac{AF^2}{AC^2}\left(1\right)\)
Ta có \(\widehat{AEB}=\widehat{AFC}=90^0\Rightarrow\Delta AEB\sim\Delta AFC\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\\ \Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AF}{AC}\right)^2=\dfrac{AF^2}{AC^2}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)

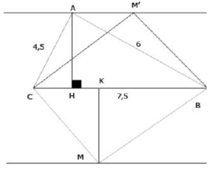
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
![]()
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
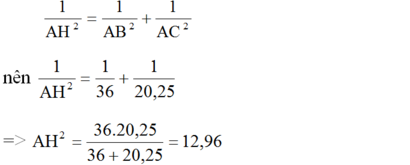
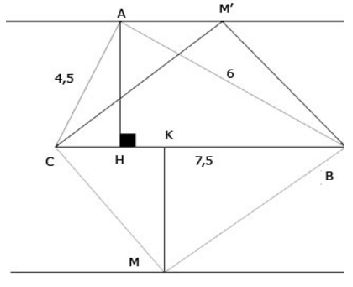
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
![]()
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).

b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.

a)ta thấy AB^2+AC^2=56.25 và BC^2=56.25
=>AB^2+BC^2=BC^2<=>tam jác ABC vuông tại A
Sin B=AC/BC=4.5/7.5<=>B=36độ 52 phút 11.63 giây (bấm shift sin 4.5/7.5 =)
sin c=AB/BC =>C=53đô 7 phút 48.37 giây
Sin C=AH/Ac =>AH=sin C*AC=3.6
b)qua A kẻ đường thẳng d song song BC.diện tích tam jác ABC luôn bằng diện tích tam jác BMC khi M thuộc d.(vì MH sẽ luôn = AH

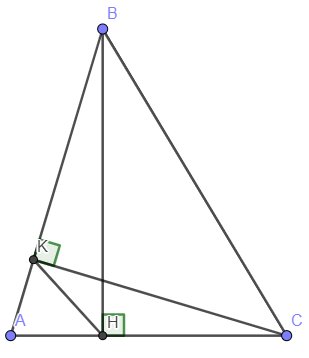

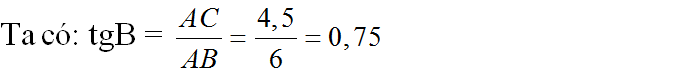
Sửa đề: Hai đường cao BD và CE. Chứng minh \(\frac{S_{ADE}}{S_{ABC}}=cos^2BAC\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\hat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\frac{AD}{AE}=\frac{AB}{AC}\)
=>\(\frac{AD}{AB}=\frac{AE}{AC}\)
Xét ΔADB vuông tại D có \(cosBAD=\frac{AD}{AB}\)
=>\(cosBAC=\frac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\frac{AD}{AB}=\frac{AE}{AC}\)
góc DAE chung
Do đó: ΔADE~ΔABC
=>\(\frac{S_{ADE}}{S_{ABC}}=\frac{AD}{AB}\cdot\frac{AE}{AC}=cosA\cdot cosA=cos^2A\)
diện tıˊch △ABE=cos2A
Lời giải ngắn gọn:
Gọi \(S\) là diện tích tam giác. Ta sẽ dùng công thức:
\(S_{\triangle A B C} = \frac{1}{2} A B \cdot A C \cdot sin \angle A\)
Gọi \(E\) là trực tâm tam giác (vì là giao của hai đường cao).
Khi đó tam giác \(A B E\) có chung đỉnh A, đáy BE.
Tuy nhiên ta xét theo tọa độ để dễ chứng minh:
Giả sử đặt tam giác \(A B C\) trong hệ trục tọa độ như sau:
Bây giờ ta cần tính:
\(\frac{S_{A B E}}{S_{A B C}} = \left(cos \right)^{2} A\)
Ta dùng kiến thức hình học không gian:
\(\frac{S_{A B E}}{S_{A B C}} = \left(cos \right)^{2} A\)
(vì tam giác \(A B E\) chiếm phần diện tích nằm trong góc A, bị chi phối bởi đường cao và tỉ lệ hình chiếu của các cạnh liên quan tới cos A)
Kết luận:
\(\frac{S_{A B E}}{S_{A B C}} = \left(cos \right)^{2} A (đ\text{pcm})\)