Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ap−1≡1(modp)<=>ap−1−1⋮p<=>ap−a⋮pap−1≡1(modp)<=>ap−1−1⋮p<=>ap−a⋮p (1)
*Nếu a là số nguyên dương Ta giả sử (1) đúng với a=n. Ta có np−n⋮pnp−n⋮p
Ta sẽ chứng minh (1) đúng với a=n+1. Thật vậy:
(n+1)p−(n+1)=np+np−1+n(n−1)2!np−2+...+n(n−1)2!n2+n+

Nhớ up tài liệu lên đây để mọi người cùng tải về nha admin VICE.

\(\Delta\)là delta, hay còn gọi là biệt thức delta, được tính bởi công thức \(\Delta=b^2-4ac\).
Trong đó \(a,b,c\)là các hệ số của phương trình: \(ax^2+bx+c=0\left(a\ne0\right)\)
Còn tại sao \(\Delta=b^2-4ac\)thì lục lại công thức nghiệm của phương trình bậc 2
Qua delta chúng ta có thể tìm được nghiệm của \(ax^2+bx+c=0\left(a\ne0\right)\).
\(\Delta< 0\)thì phương trình vô nghiệm, \(\Delta\ge0\)thì phương trình có nghiệm \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)
Delta là biệt thức. Vậy tại sao biệt thức ấy giúp bạn tìm ra nghiệm ?, tại sao nó có những đặc tính khác như vậy?
bạn trả lời theo cái cách luôn chấp nhận vô điều kiện những gì được giảng dạy, không tò mò, không sáng tạo.
Trước tiên để hiểu nó là gì, bạn cần phải hiểu phương trình bậc 2 dùng để làm gì ?
Xét ngược lại từ định lý Vi-et thì phương trình bậc 2 dùng để tìm 2 số khi biết tổng và tích của chúng, bạn có thể mở lại định lý để hiểu.
trong đó c là tích 2 nghiệm còn b là tổng 2 nghiệm
VD: PT x2 +bx + c = 0; hệ số a = 1
như đã biết giữa 2 hình CN và hình V có cùng chu vi thì hình V luôn có diện tích lớn hơn.
nên nếu (b/2)2 = c thì phương trình có nghiệm kép ngay tại điểm b/2
nếu (b/2)2 > c thì c = ((b/2) - m) x ((b/2) + m), m là khoảng cách từ 2 nghiệm tới điểm (b/2) là trung bình cộng của 2 nghiệm
<=> c = (b/2)2 - m2 <=> m 2= (b/2)2- c <=> 4m2 = b2 - 4c
mà delta = b 2- 4ac (a = 1) => delta = 4m2
mà hiệu của 2 nghiệm x1, x2 = 2 m vậy nên Delta chính là bình phương hiệu 2 nghiệm
bạn thử nhìn lại cách tìm 2 nghiệm pt xem có phải số lớn = (tổng + hiệu) /2 còn số bé là (tổng - hiệu) /2 không
với tổng là c còn hiệu là \(\sqrt{delta}\)
nói vậy chứ chẳng ai hiểu mình đâu huhu

A B C A' C' B' H a b c
\(AA'=c.sinB=b.sinC\Leftrightarrow\frac{c}{sinC}=\frac{b}{sinB}.\)
va\(BB'=c.sinA=a.sinC\Leftrightarrow\frac{c}{sinC}=\frac{a}{sinA}\)
\(\Leftrightarrow\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
\(S_{\Delta ABC}=\frac{1}{2}.a.AA'=\frac{1}{2}.a.bsinC\)

Theo đề bài ta có:
f(x) = x + x3 + x9 + x27 + x81 + x243 = Q(x).(x2 - 1) + ax + b
Thế f(1), f(-1) ta có hệ:
\(\hept{\begin{cases}a+b=6\\-a+b=-6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=6\\b=0\end{cases}}\)
Vậy a + b = 6

Tham khảo:

Chứng minh định lý hàm cos
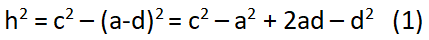
Chứng minh định lý hàm cos – Phương trình 1
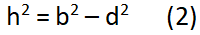
Chứng minh định lý hàm cos – Phương trình 2

Chứng minh định lý hàm cos – Phương trình 3
Với d = b cosC thế vào phương trình biến đổi (3) ta rút ra điều phải chứng minh!

Định lý Bézout (hay Định lý Bézout về các ước chung) là một kết quả quan trọng trong đại số và lý thuyết số, liên quan đến các đa thức và số nguyên.
Định lý Bézout cho rằng:
d(x)=u(x)f(x)+v(x)g(x)d(x)=u(x)f(x)+v(x)g(x)
ax+by=gcd(a,b)ax+by=gcd(a,b)
Đây là dạng cơ bản của định lý Bézout trong lý thuyết số. Định lý này được sử dụng rộng rãi trong việc tìm ước chung lớn nhất của hai số, giải quyết các phương trình Diophantine, và trong các ứng dụng mã hóa (như RSA).
Về bản chất, định lý Bézout cho phép ta biểu diễn ước chung lớn nhất của hai đa thức hoặc số nguyên dưới dạng một tổ hợp tuyến tính của chúng.
mình cần Định lý bezout về số phép chia đa thức, chứ không phải là số dư đa thức ạ.