Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được. \((x,y \in \mathbb N)\)
Số tiền bán vé thu được là: \(50000x + 100000y\) (đồng)
Rạp chiếu phim phải bù lỗ nếu: \(50000x + 100000y < 20 000 000\)
\(\Leftrightarrow x + 2y < 400\)
Vậy rạp chiếu phim phải bù lỗ nếu số vé mỗi loại thỏa mãn biểu thức \(x + 2y < 400\).

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:
9 8 15 8 20
Số trung bình: \(\overline X = \dfrac{{9 + 8 + 15 + 8 + 20}}{5} = 12\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
8 8 9 15 20
Ta có n=5 là số lẻ nên trung vị là 9.
Mốt: Ta thấy số 8 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 9=> \({Q_2} = 9\).
+ Tìm \({Q_1}\)
Nửa số liệu bên trái là:
8 8
Trung vị của mẫu này là \(\dfrac{{8 + 8}}{2} = 8\)=>\({Q_1} = 8\)
+ Tìm \({Q_3}\)
Nửa số liệu bên phải là:
15 20
Trung vị của mẫu này là \(\dfrac{{15 + 20}}{2} = 17,5\)=>\({Q_3} = 17,5\)
Vậy số trung bình là 12, trung vị là 9 và mốt là 8, \({Q_1} = 8\), \({Q_3} = 17,5\)
b) Giá của một số loại giày (đơn vị nghìn đồng):
350 300 650 300 450 500 300 250
Số trung bình: \(\overline X ) \( = \dfrac{{350 + 300.3 + 650 + 450 + 500 + 250}}{8}\) \( = 387,5\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
250 300 300 300 350 450 500 650
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 300 và 350
=> Trung vị là \(\dfrac{{300 + 350}}{2} = 325\)
Mốt: Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 325=> \({Q_2} = 325\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
250 300 300 300
Trung vị của mẫu này là \(\dfrac{{300 + 300}}{2} = 300\)=>\({Q_1} = 300\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
350 450 500 650
Trung vị của mẫu này là \(\dfrac{{450 + 500}}{2} = 475\)=>\({Q_3} = 475\)
Vậy số trung bình là 387,5, trung vị là 325 và mốt là 300, \({Q_1} = 300\), \({Q_3} = 475\)
c) Số kênh được chiếu của một số hãng truyền hình cáp:
36 38 33 34 32 30 34 35
Số trung bình: \(\overline X = \dfrac{{36 + 38 + 33 + 34.2 + 32 + 30 + 35}}{8} = 34\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
30 32 33 34 34 35 36 38
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 34 và 34
=> Trung vị là 34
Mốt: Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 34=> \({Q_2} = 34\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
30 32 33 34
Trung vị của mẫu này là \(\dfrac{{32 + 33}}{2} = 32,5\)=>\({Q_1} = 32,5\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
34 35 36 38
Trung vị của mẫu này là \(\dfrac{{35 + 36}}{2} = 35,5\)=>\({Q_3} = 35,5\)
Vậy số trung bình là 34, trung vị là 34 và mốt là 34, \({Q_1} = 32,5\), \({Q_3} = 35,5\)
Chú ý
Nếu n chẵn thì nửa số liệu bên trái (phải) \({Q_2}\) phải chứa cả \({Q_2}\)

a)
Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm (x>0)
Giá vé khi có thêm x khách là: \(800{\rm{ }}000 - 10{\rm{ }}000.x\)(đồng/người)
Doanh thu khi thêm x khách là:
\(\left( {x + 10} \right).\left( {800000 - 10000x} \right)\)\( = 10000\left( {x + 10} \right)\left( {80 - x} \right)\) (đồng)
b)
Chi phí thực sau khi thêm x vị khách là: 700 000(x+10) (đồng)
Lợi nhuận khi thêm x vị khách là:
\(T = 10000\left( {x + 10} \right)\left( {80 - x} \right)\)\( - 700000\left( {x + 10} \right)\)
\(\begin{array}{l} = 10000\left( {x + 10} \right).\left[ {80 - x - 70} \right]\\ = 10000\left( {x + 10} \right)\left( {10 - x} \right)\end{array}\)
Để công ty không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0
\(\begin{array}{l} \Leftrightarrow 10000\left( {x + 10} \right)\left( {10 - x} \right) \ge 0\\ \Leftrightarrow - 10 \le x \le 10\end{array}\)
Khi đó số khách du lịch tối đa là \(x + 10 = 10 + 10 = 20\) người thì công ty không bị lỗ.

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.

Gọi x (đồng) là giá vé người lớn, y (đồng) là giá vé trẻ em (điều kiện x > 0, y > 0). Ta có hệ phương trình:
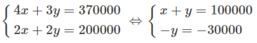
Suy ra y = 30000, x = 70000.
Vậy giá vé người lớn là 70 000 đồng, giá vé trẻ em là 30 000 đồng.

Sắp xếp lại mẫu số liệu:
20 120 20 120 21 315 23 405 37 546
Số trung bình:
\(\dfrac{{20120.2 + 21315 + 23405 + 37546}}{5}\)\( = 24501,2\)
Trung vị: 21 315
Mốt: 20 120
Nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình thì số trung bình giảm, trung vị giảm và Mốt thì vẫn giữ nguyên.
Cụ thể: số trung bình là 21 240; trung vị là 20 717,5 và Mốt vẫn là 20 120

Gọi số khách tối đa đó là m
\(\Rightarrow\)Giá vé giảm cho mỗi người là: \(\left(m-40\right).5000\) đồng
\(\Rightarrow\) Giá vé giảm cho m người là: \(m\left(m-40\right)5000=\left(m^2-40m\right).5000\) đồng
Do số tiền này ko được vượt quá 7tr nên:
\(\left(m^2-40m\right).5000\le7000000\)
\(\Leftrightarrow m^2-40m-1400\le0\)
\(\Rightarrow20-30\sqrt{2}\le m\le20+30\sqrt{2}\)
Vậy số m tối đa là 62 người



Giả sử giá vé giảm đi x$. Số lượng khán giả tăng thêm là 1000x người. Số lượng khán giả sau khi giảm giá là 9500 + 1000x người. Giá vé sau khi giảm là 14 - x$. Tổng doanh thu là (14 - x)(9500 + 1000x) = -1000x² + 4500x + 133000. Hàm số doanh thu là một hàm bậc hai với hệ số a = -1000 < 0, do đó hàm số đạt giá trị lớn nhất tại đỉnh của parabol. Hoành độ đỉnh parabol là x = -b/2a = -4500 / (2 * -1000) = 2,25. Giá vé để thu được nhiều lợi nhuận nhất là 14 - 2,25 = 11,75$.