Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=1800−12002=6002=3001800−12002=6002=300
vậy góc AMN=30độ

a) xét tam giác ABE và tam giác AFE
có BAE=EAF
BEA=FEA
AE chung
=> hai tam iác bằng nhau
b)HF=DK
HK_ chung
FHK=HKB (so le trong)
=> hai tam giác bằng nhau
xin lỗi nha nhưng câu c mình chịu ![]()
chúc bạn hok tốt!!!!!!!!!!!!

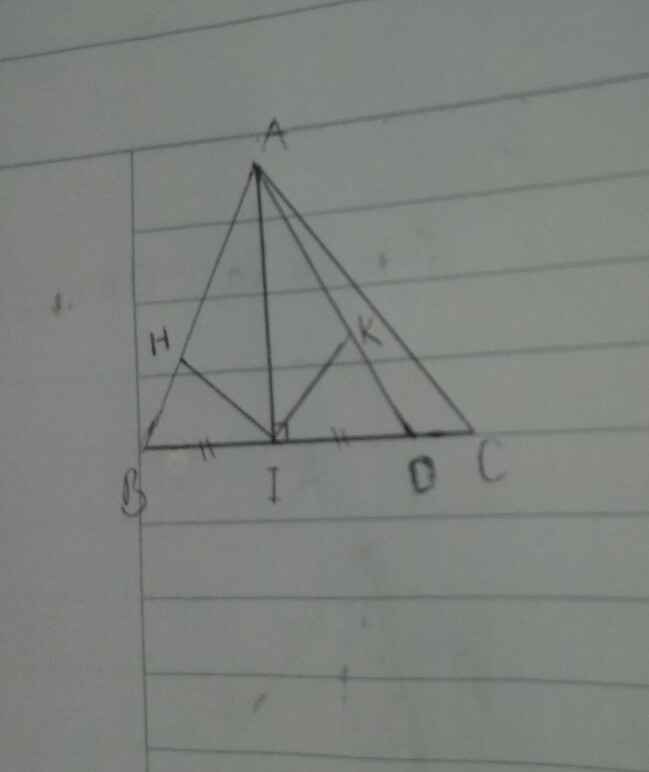
Từ I hạ IG; IK lần lượt vuông góc với AC; AB
Do BI; CI là phân giác góc và C nên IH=IG=IK
=> HC=GC=3 (cm) ; HB=KB=2 (cm)
Dễ dàng chứng minh 2 tam giác AKI và AGI là 2 tam giác vuông cân
=> IG=AG; IK=AK. Mà IH=IK=IG => AG=AK=IH=1 (cm)
=> CABC= AK+KB+HB+HC+AG+GC=1+2+2+3+1+3=12 (cm).

a) Ta áp dụng định lí Py-ta -go cho tam giác ABC vuông tại B là:
AB2 + BC2 = AC2
52 +122 =AC2
169=AC2
√169=AC
15 =AC
VẬY: AC= 15 cm
b) Xét △ABE và △DBE có:
góc DBE = góc ABE = 90( GT)
DB=AB(gt)
BE chung
➩ △ABE = △DBE (cạnh huyền - cạnh góc vuông)
➩ DE=AE (2 cạnh tương ứng bằng nhau)
➩ △EAD cân tại E (đpcm)

rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC)



a,Vì △ ABC vuông tại A ⇒∠BAC = \(90^0\)⇒∠BCA= \(180^0\) -∠ABC-\(90^0\) = \(180^0-53^0-90^0=37^0\) (tổng 3 góc trong 1△)
b,Xét △BEA và △BED có:
BE chung
AB=DB(gt)
∠ABE= ∠DBE(t/c tia pg)
=>△BEA = △BED
c,Xét △BHF và △BHC có:
BH chung
∠CBH=∠HBF(t/c tia pg)
=>△BHF = △BHC(Cạnh góc vuông-góc nhọn kề )
c, Ta có: △BHF = △BHC(cmt)=>BF = BC(2 cạnh t/ứng)
Xét △BDF và △BAC có:
∠CBH=∠HBF(t/c tia pg)
BF=BC(cmt)
=> △BDF=△BAC
d, Ta có: △BDF=tứ giác BDEA + △FEA ; △BAC = tứ giác BDEA+△CED.
Mà △BDF=△BAC(ý c) => △FEA=△CED=>∠CED=∠FEA(2 góc t/ứng)
Lại có: ∠CEF+∠CED= \(180^0\left(kềbù\right)\) , Vì ∠CED=∠FEA(cmt)=>∠CEF +∠FEA= \(180^0\left(kềnhau\right)\) nên D,E,F bắt buộc phải thẳng hàng.
Vậy D,E,F thẳng hàng(dpcm)