Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
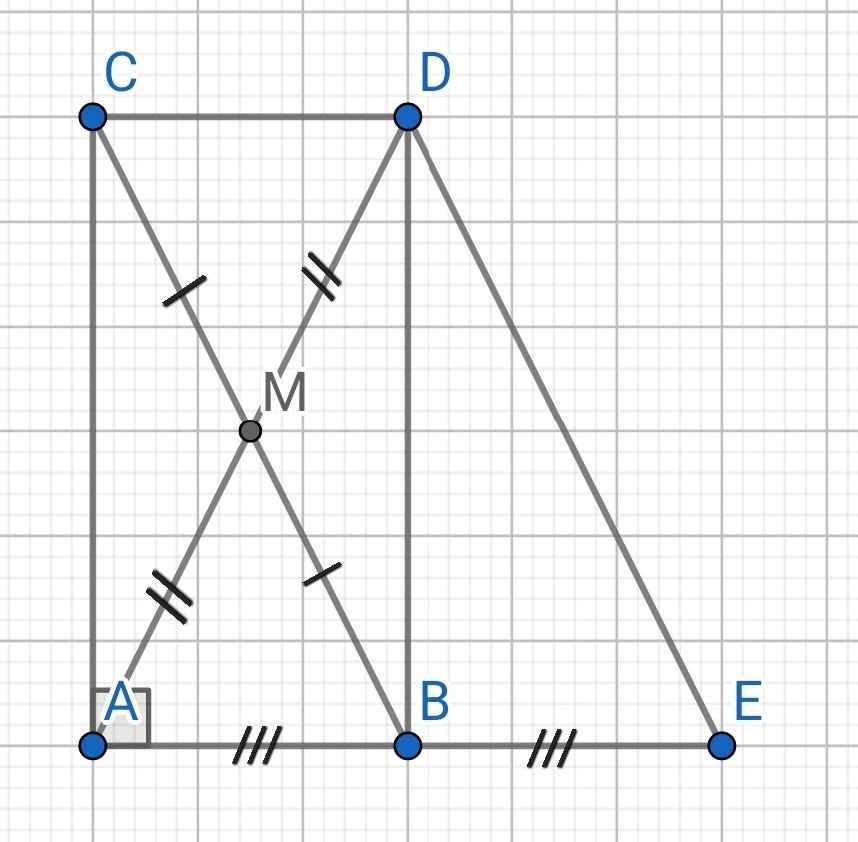a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ABDC là hình chữ nhật
=>AB//CD và AB=CD
AB=CD
AB=BE
Do đó: CD=BE
Xét tứ giác CDEB có
CD//EB
CD=EB
Do đó: CDEB là hình bình hành
c: Xét ΔADE có
DB,EM là đường trung tuyến
DB cắt EM tại K
Do đó: K là trọng tâm của ΔADE
=>EK=2KM
a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành
Để giải quyết các yêu cầu này, chúng ta sẽ lần lượt chứng minh từng phần một.
Phần a: Chứng minh ABCD là hình bình hànhTứ giác ABCD có 2 cặp cạnh đối song song và bằng nhau:
M là trung điểm của BC, tức là BM=MCBM = MC.
Trên tia đối của MA lấy điểm D sao cho MD=MAMD = MA.
Do MM là trung điểm của BCBC và MD=MAMD = MA:
MD=MA=12BCMD = MA = \frac{1}{2}BCnên AD∥BCAD \parallel BC và AD=BCAD = BC.
Như vậy, tứ giác ABCD có các cặp cạnh đối bằng nhau và song song nên ABCD là hình bình hành.
Phần b: Chứng minh BEDC là hình bình hànhĐiểm E sao cho B là trung điểm của AE:
B là trung điểm của AE tức là AB=BEAB = BE.
Chứng minh tứ giác BEDC là hình bình hành:
Để chứng minh BEDC là hình bình hành, cần chỉ ra các cặp cạnh đối song song và bằng nhau.
Tứ giác ABCD là hình bình hành nên AD \parallel BC và AD = BC.
Tứ giác BEDC là hình bình hành nếu:
BE=DC vaˋ ED∥BCBE = DC \text{ và } ED \parallel BCVì AD∥BCAD \parallel BC và AD=BCAD = BC, ta có:
AD=DC vaˋ BE=AD=DCAD = DC \text{ và } BE = AD = DCEE cũng là trung điểm của ACAC vì AA là trung điểm của BEBE.
Như vậy, BEDC là hình bình hành.
Phần c: Chứng minh AK = 2KMM cắt BD tại K:
Gọi K là giao điểm của đường thẳng AM với BD.
Do:
MlaˋtrungđiểmcủaBCM là trung điểm của BCSuy ra: AMAM là đường trung tuyến của tam giác ABCABC.
Do BDBD là đường chéo của hình bình hành, nên BDBD cắt AMAM tại điểm K.
Trong hình bình hành ABCD:
AK=2KMAK = 2KMSuy ra:
AK=2⋅KMAK = 2 \cdot KMĐiều này được chứng minh do AKAK là hai lần trung tuyến KMKM.