Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 2 là:
2.000.000 1 + 0 , 55 % 59 + 200.000 1 + 0 , 55 % 59
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 2 là:
2.000.000 1 + 0 , 55 % 58 + 200.000 1 + 0 , 55 % 58
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 3 là:
2.000.000 1 + 0 , 55 % 57 + 200.000 1 + 0 , 55 % 57
…………………………………….
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 59 là
2.000.000 1 + 0 , 55 % 1 + 200.000 1 + 0 , 55 % 1
Do đó sau 5 năm (kể từ lần gửi đầu tiên) người đó nhận được tổng số tiền cả vốn lẫn lãi là
T = 200.000. 1 + 0 , 55 % .
1 − 1 + 0 , 55 % 60 1 − 1 + 0 , 55 % + 200.000 1 + 0 , 55 % 59
1 + 2 1 + 0 , 55 % − 1 + 3 1 + 0 , 55 − 2 + ...59 1 + 0 , 55 − 58
Mặt khác ta có:
x + x 2 + x 3 + ... + x n = x 1 − x n 1 − x = x − x n + 1 1 − x
Đạo hàm 2 vế ta có:
1 + 2 x + 3 x 2 + ... + n x n − 1 = 1 − n + 1 x n 1 − x + x − x n − 1 1 − x
Với x = 1 1 + 0 , 55 ; n = 59 ta có:
1 + 2 1 + 0 , 55 % − 1 + 3 1 + 0 , 55 − 2 + ....59 1 + 0 , 55 − 58 ≈ 1436
Vậy T = 539447312 đồng

Đáp án C
Gọi số tiền ban đầu là A đồng, ta có 1 + 6 % 10 − A = 100 ⇒ A ≈ 1264465989 đồng.


= 100 1 , 006 3 - 0 , 5 + 0 , 5 1 , 006 + 0 , 5 1 , 006 2 ;

= 100 1 , 006 36 - 0 , 5 + 0 , 5 1 , 006 0 , 5 + . . . + 0 , 5 1 , 006 35


Đáp án A.


Gọi B là số tiền của người đó trong tài khoản tiết kiệm đến hết tháng 12 năm 2020. Khi đó n = 24
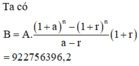

Chọn C
Gọi A là số tiền gửi ban đầu, n là số năm gửi.
Theo bài ra: Sau 1 năm, số tiền cả vốn lẫn lãi là : A + A. 8,4% =A. 1,084.
Sau 2 năm, số tiền cả vốn lẫn lãi là: A.1,084 + A. 1,084.8,4% = A. 1,084^2.
Sau n năm, số tiền cả vốn lẫn lãi là A. 1,084^n.
Số tiền này bằng 2 lần ban đầu nên: A. 1,084^n = 3A
ð n = ~ 14
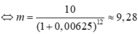





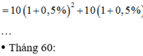


Gọi A ( đồng), r(%) lần lượt là số tiền người đó gửi và lãi suất hàng tháng
Đk: 150000>A>0; r>0
Theo đề bài, ta có:
\(\left\{{}\begin{matrix}Ar=150000 \\A\left(1+r\right)r=301200\end{matrix}\right.\)
\(\left\{{}\begin{matrix}A=\dfrac{150000}{x}\\A=\dfrac{301200}{\left(1+r\right)r}\end{matrix}\right.\)
⇒\(\dfrac{150000}{r}=\dfrac{301200}{\left(1+r\right)r}\)
Giải phương trình trên ta được:
r=1,008
mà Ar=150000
⇒A=\(\dfrac{150000}{r}\approx148810\)
Vậy