K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
2 tháng 8 2017
Lời giải:
PT hoành độ giao điểm:
\(x+m-\frac{2x-1}{x-1}=0\Leftrightarrow x^2+x(m-3)+(1-m)=0\) \((1)\)
Để hai ĐTHS cắt nhau ở hai điểm thì PT $(1)$ phải có hai nghiệm phân biệt \(\Leftrightarrow \Delta=(m-3)^2-4(1-m)>0\Leftrightarrow (m-1)^2+4>0\)
(luôn đúng với mọi $m$ )
Khi đó với \(x_1,x_2\) là hai nghiệm của PT trên thì \(A(x_1,x_1+m) ; B(x_2,x_2+m)\) là hai giao điểm của 2 ĐTHS.
Không mất tổng quát, giả sử tam giác $OAB$ vuông tại $A$
\(\Rightarrow \overrightarrow{OA}\perp \overrightarrow{AB}\Leftrightarrow (x_1,x_1+m)\perp (x_2-x_1,x_2-x_1)\)
\(\Leftrightarrow x_1(x_2-x_1)+(x_2-x_1)(x_1+m)=0\)
\(\Rightarrow 2x_1+m=0\Rightarrow x_1=\frac{-m}{2}\)
Mà áp dụng định Viete: \(\left\{\begin{matrix} x_1+x_2=3-m\\ x_1x_2=1-m\end{matrix}\right.\Rightarrow x_1=3-m-x_1=\frac{1-m}{x_1}\)
\(\Leftrightarrow 3-\frac{m}{2}=\frac{2(m-1)}{m}\Rightarrow m=1\pm \sqrt{5}\) (thỏa mãn )
Vậy \(m=1\pm \sqrt{5}\)
12 tháng 5 2016
Ta có \(a=\log_{\sqrt{2}}\left(\frac{1}{\sqrt[3]{5}}\right)=\log_{2^{\frac{1}{2}}}5^{-\frac{1}{3}}=-\frac{2}{3}\log_25\)
\(\Rightarrow\log_25=-\frac{3a}{2}\)
\(\Rightarrow C=\log40=\frac{\log_240}{\log_210}=\frac{\log_2\left(2^3.5\right)}{\log_2\left(2.5\right)}=\frac{3+\log_25}{1+\log_25}=\frac{6-3a}{2-3a}\)
17 tháng 9 2016
Gọi \(S_n\) là cách thỏa ycđp
Muốn lên và xuống thang n bậc \(\left(n>3\right)\) có 3 cách :
- Bước tới bậc n-1 rồi bước 1 bậc để lên n và xuống 1 bậc: 1 cách.
- Bước tới bậc n-2 rồi bước 2 bậc để lên n, sau đó xuống 2 bậc hoặc bước lên tửng bậc, xuống từng bậc hoặc xuống 2 bậc: 3 cách.
- Bước tới bậc n-3 để lên n rồi xuống thang: 9 cách (lấy theo VD cho nhanh).
Ta có hệ thức truy hồi, với \(n>3\)3
\(S_n=S_{n-1}+S_{n-2}+S_{n-3}\)
Khởi tạo : \(S_1=1,S_2=3,S_3=9\)
Suy ra : \(S_{11}=157+289+531=977\) cách .
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 3 2019
1/Áp dụng công thức tổng cấp số nhân:
\(z=1+\left(1+i\right)+\left(1+i\right)^2+...+\left(1+i\right)^{20}=1+\frac{\left(1+i\right)^{21}-1}{i+1-1}=1+\frac{\left(1+i\right)^{21}-1}{i}\)
Ta có:
\(\left(1+i\right)^{21}=\left(1+i\right)\left[\left(1+i\right)^2\right]^{10}=\left(1+i\right)\left(1+2i+i^2\right)^{10}\)
\(=\left(1+i\right)\left(2i\right)^{10}=\left(1+i\right).2^{10}.i^{10}=\left(1+i\right)2^{10}\left(i^2\right)^5=-\left(1+i\right).2^{10}\)
\(\Rightarrow z=1+\frac{-\left(1+i\right)2^{10}-1}{i}=1+\frac{-i\left(1+i\right)2^{10}-i}{i^2}=1+\left(i+i^2\right)2^{10}+i=1+i+\left(i-1\right).2^{10}\)
\(\Rightarrow z=\left(1-2^{10}\right)+\left(1+2^{10}\right)i\)
2/
\(z=\left(3+i\sqrt{3}\right)^3\Rightarrow\frac{1}{z}=\frac{1}{\left(3+i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(3+i\sqrt{3}\right)^3\left(3-i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(9-3i^2\right)^3}\)
\(\Rightarrow\frac{1}{z}=\frac{\left(3-i\sqrt{3}\right)^3}{12^3}=\left(\frac{1}{4}-\frac{\sqrt{3}}{12}i\right)^3\)
3/ Bạn viết lại đề được không?
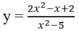
moihhfthmfyhuedmtfcgbvxdsfrwmetyh
Nhà em có 2345 con gà,1234 con vịt. Hỏi nhà em có tất cả bao nhiêu con?