
a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)


a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
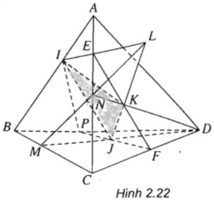
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)

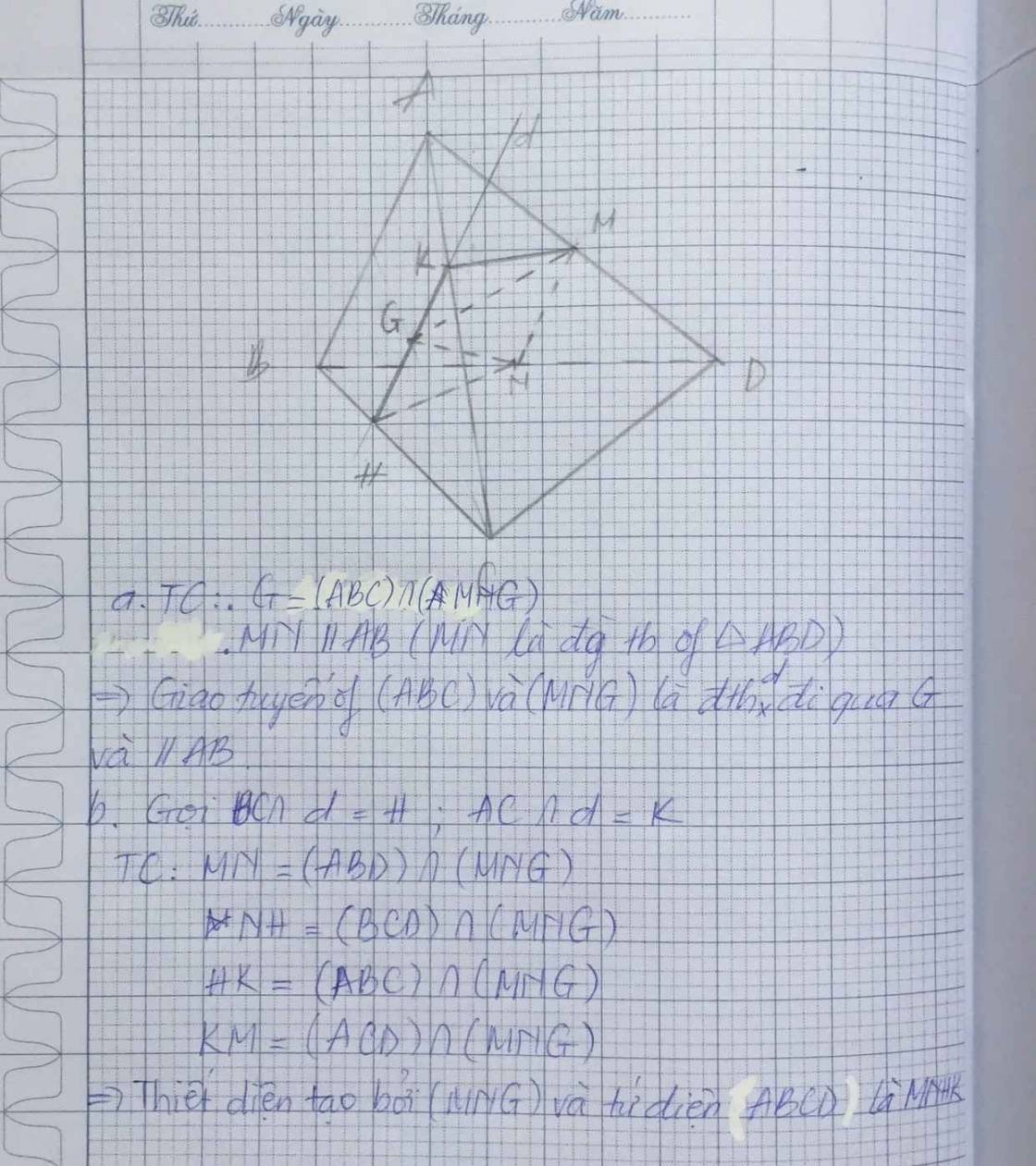
G là điểm chung của hai mặt phẳng (ABC) và (MNG).
Ta có BC // MN (Do MN là đường trung bình của tam giác ABD).
Vậy giao tuyến của hai mặt phẳng (ABC) và (MNG) là đường thẳng d đi qua G song song với BC.
Trong (ABC): d \cap∩ BC = P
d \cap∩ AC = QVậy thiết diện cần tìm là tứ giác MNPQ.

Gọi I là trung điểm CD thì G 1 ∈ B I , G 2 ∈ A I ⇒ mặt phẳng ( B G 1 G 2 ) chính là mặt phẳng (ABI) ⇒ Thiết diện là tam giác cân AIB.
Đáp án C

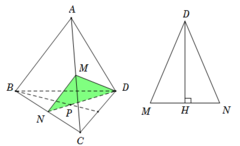
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.

1. Định nghĩa các điểm:
2. Tính toán giao điểm:
-
-
-
-
-
b) Tìm thiết diện của tứ diện cắt bởi mặt phẳng (EMN)(EMN)(EMN)Trọng tâm của tam giác: Trọng tâm của tam giác là điểm giao của ba đường trung tuyến. Trong tam giác ABCABCABC, trọng tâm MMM là điểm mà ba đường trung tuyến cắt nhau, và MMM chia mỗi đường trung tuyến theo tỷ lệ 2:1 tính từ đỉnh.
Điểm NNN tương tự, là trọng tâm của tam giác ABDABDABD, nên nó cũng nằm trên đường trung tuyến của tam giác ABDABDABD.
Điểm EEE thuộc mặt phẳng (BCD)(BCD)(BCD).
Mặt phẳng (EMN)(EMN)(EMN) là mặt phẳng chứa điểm EEE, trọng tâm MMM của tam giác ABCABCABC, và trọng tâm NNN của tam giác ABDABDABD.
Mặt phẳng (BCD)(BCD)(BCD) là mặt phẳng chứa ba điểm BBB, CCC, và DDD.
Để xác định giao điểm của hai mặt phẳng, ta cần biết điểm cụ thể của mặt phẳng (EMN)(EMN)(EMN) nằm trong mặt phẳng (BCD)(BCD)(BCD).
Giao điểm của hai mặt phẳng này có thể được tính toán bằng cách xác định mặt phẳng (EMN)(EMN)(EMN) và mặt phẳng (BCD)(BCD)(BCD) từ tọa độ của các điểm EEE, MMM, NNN và các điểm trong mặt phẳng (BCD)(BCD)(BCD).
Tuy nhiên, trong bài toán này, với thông tin có sẵn, bạn có thể thấy rằng điểm giao của hai mặt phẳng này nằm trên mặt phẳng BCDBCDBCD và do đó giao điểm sẽ là điểm mà mặt phẳng (EMN)(EMN)(EMN) cắt mặt phẳng (BCD)(BCD)(BCD).
1. Xác định mặt phẳng (EMN)(EMN)(EMN):