K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SC
12 tháng 1 2022
tích vô hướng của 2 vecto AB và AC = tích độ dài . Cos góc xen giữa:
= 5 . 5 cos(120) = -25/2
Ngủ đi bạn
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
ĐKXĐ: \(x>3\)
\(\Leftrightarrow2x+2\sqrt{x-3}\sqrt{x+3}=\dfrac{4\left(x+3\right)}{\left(x-3\right)^2}\)
\(\Leftrightarrow\left(\sqrt{x+3}+\sqrt{x-3}\right)^2=\dfrac{4\left(x+3\right)}{\left(x-3\right)^2}\)
\(\Leftrightarrow\sqrt{x+3}+\sqrt{x-3}=\dfrac{2\sqrt{x+3}}{x-3}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x+3}-\sqrt{x-3}}=\dfrac{\sqrt{x+3}}{x-3}\)
\(\Leftrightarrow3x-9=x+3-\sqrt{x^2-9}\)
\(\Leftrightarrow\sqrt{x^2-9}=12-2x\) (\(x\le6\))
\(\Leftrightarrow x^2-9=144-48x+4x^2\)
\(\Leftrightarrow3x^2-48x+153=0\)
\(\Leftrightarrow x=8-\sqrt{13}\)
NL
2
NL
1
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
8 tháng 7 2021
Để bpt luôn đúng với mọi \(x\in R\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow9-4\left(m-2\right)\le0\)\(\Leftrightarrow m\ge\dfrac{17}{4}\)
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 12 2021
d là khẳng định sai
Hai vecto \(\overrightarrow{a};\overrightarrow{b}\) không cùng phương nên không ngược hướng
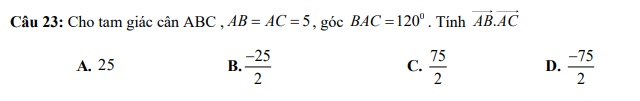
bn hỏi jv, sao mik ko thấy
???