Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có
.
.
Hình bên dưới là đồ thị của hàm số 
và 
.
Dựa vào hình vẽ ta thấy đồ thị hàm số 
và 
cắt nhau tại 2 điểm phân biệt, đồng thời 
khi 
hoặc 
, 
khi 
.
Do đó 
đổi dấu qua 
, 
.
Vậy hàm số g(x) có hai điểm cực trị.
a.
TXĐ: \(D=\left[-4;2\right]\)
\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)
\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)
\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)
Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)
\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)
(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)
b.
\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:
\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:
Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu
Hàm đồng biến trên ... bạn tự kết luận
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị
Chọn D.
Xét g(x) = f x 2 - 2
Bảng xét dấu g’(x):
Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.
Chọn B
+ Dựa vào đồ thị hàm số ta thấy :
- Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; 1) và ( 3; 5) .
- Hàm số y= f( x) nghịch biến trên khoảng ( 1 ; 3) và ( 5 ; + ∞)
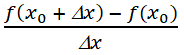
Đáp án: D.3
Giải thích:
Để tìm cực trị của hàm hợp \( g(x) = f(x^2 - 2x - 1) \), ta cần thực hiện các bước sau:
1. Tìm điểm cực trị của hàm số \( f(x^2 - 2x - 1) \).
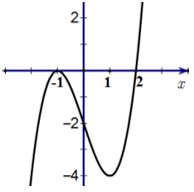
2. Phân tích số điểm cực trị của \( f(x^2 - 2x - 1) \) dựa trên đồ thị của \( f'(x) \).
Trước hết, để tìm điểm cực trị của hàm số \( f(x^2 - 2x - 1) \), ta cần tìm đạo hàm của \( g(x) \), sau đó giải phương trình \( g'(x) = 0 \) để tìm các điểm mà đạo hàm bằng 0.
Đạo hàm của \( g(x) = f(x^2 - 2x - 1) \):
\[ g'(x) = f'(x^2 - 2x - 1) \cdot (2x - 2) \]
Bây giờ, ta cần giải phương trình \( g'(x) = 0 \) để tìm điểm mà \( g(x) \) có đạo hàm bằng 0:
\[ f'(x^2 - 2x - 1) \cdot (2x - 2) = 0 \]
Điều này có nghĩa là hoặc \( f'(x^2 - 2x - 1) = 0 \) hoặc \( 2x - 2 = 0 \).
\( 2x - 2 = 0 \) khi \( x = 1 \).
Sau khi tìm \( x \), ta cần kiểm tra xem các giá trị của \( x \) khi đặt vào \( f'(x^2 - 2x - 1) \) tạo ra bao nhiêu điểm cực trị trên đồ thị của \( f'(x) \). Số lượng điểm cực trị của hàm số \( f(x) \) khi nhân với hệ số 2x-2 là số lượng điểm cực trị của hàm số \( f(x) \) bị tịnh tiến sang phải 1 đơn vị. Điều này có nghĩa là số điểm cực trị của \( g(x) \) sẽ giống với số điểm cực trị của \( f(x) \).
Vậy, đáp án là \(\mathbf{D. 3}\).
P/s: Lỗi font hơi nhiều
Từ đồ thị \(\Rightarrow\) hàm \(f\left(x\right)\) có 1 cực trị tại \(x=2\)
\(g'\left(x\right)=\left(2x-2\right).f'\left(x^2-2x-1\right)\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}2x-2=0\\f'\left(x^2-2x-1\right)=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x^2-2x-1=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
Vậy hàm \(g\left(x\right)\) có 3 cực trị