Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

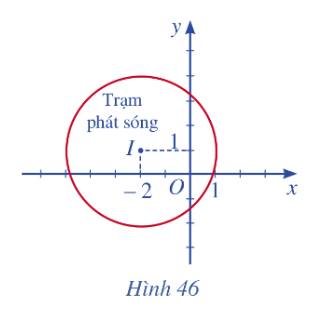
a) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)

a) Đúng. Mệnh đề phủ định: "1794 không chia hết cho 3".
b) Sai. "√2 không phải là một số hữu tỉ".
c) Đúng. "π không nhỏ hơn 3, 15". Dùng kí hiệu là: π ≥ 3,15 .
d) Sai. "|-125|>0".
a) Mệnh đề đúng.
Phủ định là " \(\sqrt{3}+\sqrt{2}\ne\dfrac{1}{\sqrt{3}-\sqrt{2}}\), mệnh đề này sai
b) Mệnh đề sai, vì \(\left(\sqrt{2}-\sqrt{18}\right)^2=8\).
Phủ định là " \(\left(\sqrt{2}-\sqrt{18}\right)^2\le8\)", mệnh đề này đúng
c) Mệnh đề đúng, vì \(\left(\sqrt{3}+\sqrt{12}\right)^2=27\)
Phủ định là "\(\left(\sqrt{3}+\sqrt{12}\right)^2\) là một số vô tỉ", mệnh đề này sai
d) Mệnh đề sai
Phủ định là " \(x=2\) không là nghiệm của phương trình \(\dfrac{x^2-4}{x-2}=0\)", mệnh đề này đúng

a) \(\overline{P}\) là mệnh đề " 15 chia hết cho 3"; P sai, \(\overline{P}\) đúng
b) \(\overline{Q}\) là mệnh đề "\(\sqrt{2}\le1\)"; Q đúng, \(\overline{Q}\) sai

a) \(MA^2+MB^2=MC^2\)
\(\Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 4} \right)^2} + {\left( {y + 2} \right)^2}\)
\(\Leftrightarrow {x^2} + {y^2} + 12x - 10y - 5 = 0\)
\(\Leftrightarrow {\left( {x + 6} \right)^2} + {\left( {y - 5} \right)^2} = 66\)
Vậy tập hợp các điểm M là một đường tròn.
b) Tâm là điểm (-6 ; 5) bán kính bằng \(\sqrt{66}\)

T M P I 3
gọi T ;P là 2 tiếp điểm của 2 tiếp tuyến kẻ từ M đến đường tròn (C)
\(\Delta MTP\) cận tại M (t/c tt)\(\Rightarrow MO\) là tia phân giác ;đường cao ...
\(\Rightarrow\widehat{TMO}=\widehat{PMO}=60^0\left(gt\right)\)
\(\Delta TMO\) có \(\widehat{MTO}=90^0\left(tt\right)\)\(\Rightarrow\Delta TMO\) là tam giác nửa đều
\(\Rightarrow MO=2TO=2.3=6\)
vậy tập hợp những điểm M cách đều điểm I(1;2) 1 khoảng cố định=6 là đường tròn tâm I(1;2) và bán kính R=6.
PT duong tron (C') \(\left(x-1\right)^2+\left(y-2\right)^2=36\).

vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv⚽☺
tttuuuu==+0__$$$TTT❤