NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
22 tháng 9 2018
gọi Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
dễ dàng nhận thấy AP // CM vì góc DAP = góc BCM. Tương tự ta có EF//HG
vậy tứ giác EFGH là hình bình hành
Vì ABCD là hình bình hành nên
góc B+C = 180
xét tam giác CGB
có góc B+C = 180 : 2 = 90 vậy góc G = 90
xét hình bình hành EFGH có 1 góc vuông nên đó là hình chữ nhật
16 tháng 8 2019
\(\left(\Sigma\frac{1}{\left(a+b\right)^2}\right)\left(2abc+\Sigma a^2\left(b+c\right)\right)=\Sigma\frac{a\left(b+c\right)^2+\left(a^2+bc\right)\left(b+c\right)}{\left(b+c\right)^2}=\Sigma a+\Sigma\frac{a^2+bc}{b+c}\)
Mặt khác ta có :
\(\left(\Sigma\frac{a^2+bc}{b+c}\right)\left(\Sigma a\right)=\Sigma\frac{a^3+abc}{b+c}+\Sigma\left(a^2+bc\right)\) ( nhân vào xong tách )
\(=\Sigma\frac{a^3+abc}{b+c}-\Sigma a^2+\Sigma\left(2a^2+bc\right)=\Sigma\frac{a\left(a-b\right)\left(a-c\right)}{b+c}+\Sigma\left(2a^2+bc\right)\) ( * )
Theo BĐT Vornicu Schur chứng minh được ( * ) không âm.
do đó : \(\Sigma\frac{a^2+bc}{b+c}\ge\frac{\Sigma\left(2a^2+bc\right)}{\Sigma a}\)
Theo đề bài , cần chứng minh : \(\left(\Sigma ab\right)\left(\Sigma\frac{1}{\left(a+b\right)^2}\right)\ge\frac{9}{4}\)
Kết hợp với dòng đầu tiên t cần c/m :
\(\left(\Sigma ab\right)\left(\Sigma a+\frac{\Sigma\left(2a^2+bc\right)}{\Sigma a}\right)\ge\frac{9}{4}\left(2abc+\Sigma a^2\left(b+c\right)\right)\)
Quy đồng lên, ta được :
\(\Sigma a^3\left(b+c\right)\ge2\Sigma\left(ab\right)^2\Leftrightarrow\Sigma ab\left(a-b\right)^2\ge0\)
\(\Rightarrow\)đpcm
L
23 tháng 10 2019
Bài này lằng nhằng quá. Thôi kệ làm thử phát :>
(1)Ta có:
\(\frac{9}{5}=1+\frac{4}{5}=\frac{1}{2}+\frac{1}{2}+\frac{4}{5}\)
Vì \(\frac{1}{2}>\frac{1}{5};\frac{1}{3}>\frac{1}{5};...;\frac{1}{5}=\frac{1}{5}\)
\(\Rightarrow\frac{1}{2}+\frac{1}{3}+...+\frac{1}{5}>\frac{1}{5}.4=\frac{4}{5}\)
Vì \(\frac{1}{6}>\frac{1}{10};\frac{1}{7}>\frac{1}{10};...;\frac{1}{10}=\frac{1}{10}\)
\(\Rightarrow\frac{1}{6}+\frac{1}{7}+...+\frac{1}{10}>\frac{1}{10}.5=\frac{1}{2}\)
\(\frac{1}{11}>\frac{1}{20};\frac{1}{12}>\frac{1}{20};...;\frac{1}{20}=\frac{1}{20}\)
\(\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}>\frac{1}{20}.10=\frac{1}{2}\)
Từ trên \(\Rightarrow\frac{9}{5}< A\)
(2)Ta có:
\(\frac{25}{6}=4+\frac{1}{6}=3+\frac{1}{2}+\frac{1}{2}+\frac{1}{6}\)
Có được \(\frac{1}{2}=\frac{1}{2}\)
Vì \(\frac{1}{3}=\frac{1}{3};\frac{1}{4}< \frac{1}{3};..\frac{1}{11}< \frac{1}{3}\)
\(\Rightarrow\frac{1}{3}+\frac{1}{4}+...+\frac{1}{11}< \frac{1}{3}.9=3\)
Vì \(\frac{1}{12}=\frac{1}{12};\frac{1}{13}< \frac{1}{12}\)
\(\Rightarrow\frac{1}{12}+\frac{1}{13}< \frac{1}{12}.2=\frac{1}{6}\)
Vì \(\frac{1}{14}=\frac{1}{14};\frac{1}{15}< \frac{1}{14};...\frac{1}{20}< \frac{1}{14}\)
\(\Rightarrow\frac{1}{14}+\frac{1}{15}+...+\frac{1}{20}< \frac{1}{14}.7=\frac{1}{2}\)
Từ trên \(\Rightarrow A< \frac{25}{6}\)
Từ (1) và (2)
\(\Rightarrowđpcm\)
DH
23 tháng 10 2019
Bạn j ở trên ơi? Bạn làm vừa dài vừa khó hiểu vậy thì bạn kia làm sao mà hiểu được. Ngay cả mị còn ko hiểu. Bài của bạn nhìn sai bét rồi còn gì. Làm thế chỉ mỏi tay mà thôi. Còn đây là cách của mị
Bài này họ không bảo là tính nhanh lên bạn cứ tính tổng cộng tất cả rồi so sánh và kết luận ra ý. Mà mị cũng không chắc nữa. Nhưng bạn cứ làm theo mị ấy bài kia làm mỏi tay lắm. Làm thì phải ngắn chứ.
Dark horse cute thông minh
Mị lớp 10 nên học qua rồi
KP
2 tháng 5 2022
cho mình hỏi đề bạn viết có đúng không vậy
Cho △ABC vuông tại A (AB<AC) có đường cao AH
a) Chứng minh : △HBA=△ABC ( chứng minh kiểu gì)
b)Chứng minh: AH2=HB.HC
c)Gọi E là điểm đối xứng với H qua điểm A, M là trung điểm của AH. Chứng minh CM⊥BE tại K
7 tháng 9 2015
Với a,b >0.Ta có: \(\frac{1}{a}+\frac{1}{b}\ge\frac{\left(1+1\right)^2}{a+b}=\frac{4}{a+b}\left(đpcm\right)\)
Dấu = xảy ra khi và chỉ khi a=b
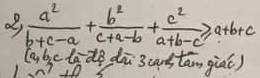
Áp dụng BĐT \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}\)(a,b,c,x,y,z > 0)
Vì a,b,c là độ dài 3 cạnh của tam giác nên a,b,c > 0
Áp dụng BĐT tam giác, ta có a < b + c, b < c + a, c < a + b
=> b + c - a, c + a - b, a + b - c > 0
Khi đó, ta có \(\dfrac{a^2}{b+c-a}+\dfrac{b^2}{c+a-b}+\dfrac{c^2}{a+b-c}\ge\dfrac{\left(a+b+c\right)^2}{a+b+c}=a+b+c\)
(đpcm).Dấu = xảy ra <=> a = b = c