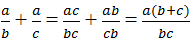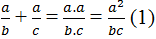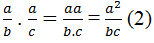Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.a.ta có:\(\frac{2017+2018}{2018+2019}=\frac{2017}{2018+2019}+\frac{2018}{2018+2019}\)
mà \(\frac{2017}{2018}>\frac{2017}{2018+2019};\frac{2018}{2019}>\frac{2018}{2018+2019}\)
\(\Rightarrow M>N\)
b.ta thấy:
\(\frac{n+1}{n+2}>\frac{n+1}{n+3}>\frac{n}{n+3}\Rightarrow\frac{n+1}{n+2}>\frac{n}{n+3}\)
=> A>B

Ta có:
Mà a = b + c nên
Từ (1), (2) suy ra:
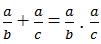

a) \(A=\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}\)
\(\Rightarrow A< \frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{99\cdot100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{100}< \frac{1}{2}\)
b) b = a - c => b + c = a
\(\left\{{}\begin{matrix}\frac{a}{b}\cdot\frac{a}{c}=\frac{a^2}{bc}\\\frac{a}{b}+\frac{a}{c}=\frac{ac+ab}{bc}=\frac{a\left(b+c\right)}{bc}=\frac{a^2}{bc}\end{matrix}\right.\)
\(\Rightarrow\frac{a}{b}\cdot\frac{a}{c}=\frac{a}{b}+\frac{a}{c}\)
Bước 2 bạn sai rồi. Vd: \(\frac{1}{3x3}\) đâu bằng hay nhỏ hơn \(\frac{1}{2x3}\)

Giải
\(\frac{a}{-b}=\frac{-a}{b}\text{ vì }ab=\left(-b\right)(-a)\)
\(\frac{-a}{-b}=\frac{a}{b}\text{ vì }\left(-a\right)b=\left(-b\right)a\)
Okay !

a) \(\frac{a}{-b}=\frac{a.\left(-1\right)}{-b.\left(-1\right)}=\frac{-a}{b}\)
\(\Rightarrow\frac{a}{-b}=\frac{-a}{b}\)
b) \(\frac{-a}{-b}=\frac{-a.\left(-1\right)}{-b.\left(-1\right)}=\frac{a}{b}\)
\(\Rightarrow\frac{-a}{-b}=\frac{a}{b}\)
a) Ta có:
\(\frac{a}{-b}=\frac{a.\left(-1\right)}{-b.\left(-1\right)}=\frac{-a}{b}\)
\(\Rightarrow\frac{a}{-b}=\frac{-a}{b}\)
b) Ta có:
\(\frac{-a}{-b}=\frac{-a.\left(-1\right)}{-b.\left(-1\right)}=\frac{a}{b}\)
\(\Rightarrow\frac{-a}{-b}=\frac{a}{b}\)