Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)

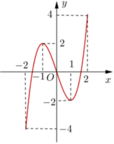
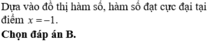
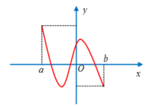
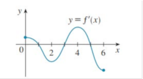


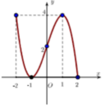
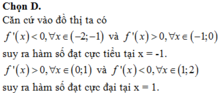
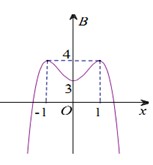
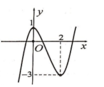

Chọn B
Phương pháp: Dựa vào đồ thị hàm số.
Cách giải: Chọn B.