Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AH=\sqrt{25\cdot64}=40\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(\tan B=\dfrac{AH}{HB}=\dfrac{40}{25}=1.6\)
nên \(\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)

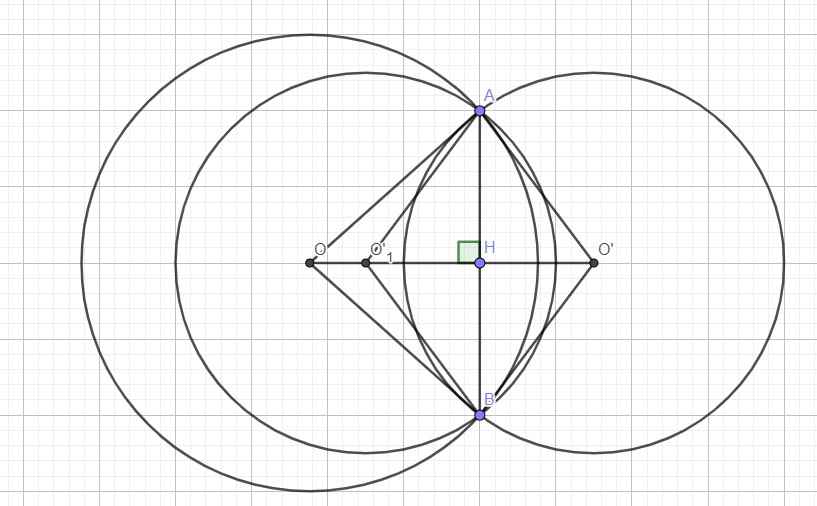
(O) và (O') có 2 vị trí tương đối như hình vẽ, tâm O' có thể nằm ở O' hoặc \(O'_1\)
Gọi H là giao điểm AB và OO', theo tính chất 2 đường tròn cắt nhau ta có H là trung điểm AB và \(OO'\perp AB\)
\(\Rightarrow AH=BH=\dfrac{AB}{2}=4\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông OAH:
\(OH=\sqrt{OA^2-AH^2}=\sqrt{6^2-4^2}=2\sqrt{5}\)
Pitago cho tam giác vuông O'AH:
\(O'H=\sqrt{O'A^2-AH^2}=\sqrt{5^2-4^2}=3\)
\(\Rightarrow\left[{}\begin{matrix}OO'=OH+O'H=2\sqrt{5}+3=7,47\\OO'=OH-O'H=2\sqrt{3}-3=1,47< 2\left(loại\right)\end{matrix}\right.\)

1: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}+47^0=90^0\)
=>\(\widehat{C}=43^0\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(BC=\dfrac{10}{sin43}\simeq14,66\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{BC^2-AB^2}\simeq10,72\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
=>\(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot CB}=\dfrac{BH}{CH}\)
Xét ΔHAB vuông tại H có HD là đường cao
nên \(BD\cdot BA=BH^2\)
=>\(BD=\dfrac{BH^2}{AB}\)
Xét ΔHAC vuông tại H có HE là đường cao
nên \(CE\cdot CA=CH^2\)
=>\(CE=\dfrac{CH^2}{AC}\)
\(\dfrac{BD}{EC}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}\)
\(=\left(\dfrac{BH}{CH}\right)^2\cdot\dfrac{AC}{AB}=\left(\dfrac{AB^2}{AC^2}\right)^2\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^3}{AC^3}\)